19、(本题满分14分)已知函数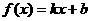 的图象与
的图象与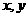 轴分别相交于点A、B,
轴分别相交于点A、B,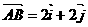 (
(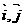 分别是与
分别是与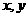 轴正半轴同方向的单位向量),函数
轴正半轴同方向的单位向量),函数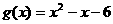 .
.
(1)求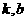 的值;
的值;
(2)当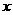 满足
满足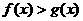 时,求函数
时,求函数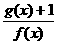 的最小值.
的最小值.
[思路点拨]本题是以向量为背景,解析法为手段,考查解析思想的运用和处理函数性质的方法,考查运算能力和运用数学模型的能力.
[正确解答] (1)由已知得A(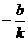 ,0),B(0,b),则
,0),B(0,b),则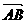 ={
={ ,b},于是
,b},于是 =2,b=2. ∴k=1,b=2.
=2,b=2. ∴k=1,b=2.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
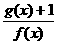 =
=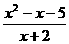 =x+2+
=x+2+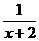 -5
-5
由于x+2>0,则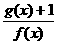 ≥-3,其中等号当且仅当x+2=1,即x=-1时成立
≥-3,其中等号当且仅当x+2=1,即x=-1时成立
∴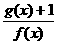 的最小值是-3.
的最小值是-3.
[解后反思]要熟悉在其函数的定义域内,常见模型函数求最值的常规方法.如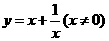 型.
型.
- 答案

