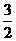16.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则点P到AC、BC
的距离乘积的最大值是
解:P到BC的距离为d1,P到AC的距离为d2,则三角形的面积得3d1+4d2=12,∴3d1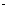 4d2≤
4d2≤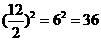 ,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=
,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=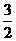
- 答案
16.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则点P到AC、BC
的距离乘积的最大值是
解:P到BC的距离为d1,P到AC的距离为d2,则三角形的面积得3d1+4d2=12,∴3d1 4d2≤
4d2≤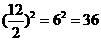 ,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=
,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=