21．(本小题满分12分)

已知数列

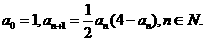
(1)证明

(2)求数列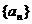的通项公式a_n.

[思路点拨]本题考查数列的基础知识，考查运算能力和推理能力.第(1)问是证明递推关系，联想到用数学归纳法，第(2)问是计算题，也必须通过递推关系进行分析求解.

[正确解答](1)方法一 用数学归纳法证明：

1°当n=1时，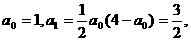

　 ∴，命题正确.

2°假设n=k时有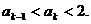

　 则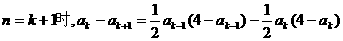

而

又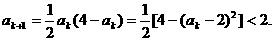

∴时命题正确.

由1°、2°知，对一切n∈N时有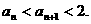

方法二：用数学归纳法证明：

　　 1°当n=1时，∴；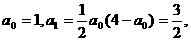

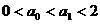　　 2°假设n=k时有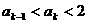成立，

　　　 令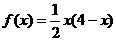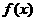，在[0，2]上单调递增，所以由假设

有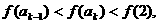：即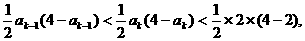

也即当n=k+1时　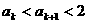 成立，所以对一切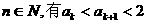

　 (2)下面来求数列的通项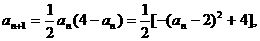：所以

,

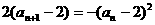
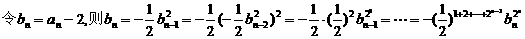又b_n=－1，所以.

[解后反思]数列是高考考纲中明文规定必考内容之一,考纲规定学生必须理解数列的概念,了解数列通项公式的意义,了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.当然数列与不等式的给合往往得高考数学的热点之一,也成为诸多省份的最后压轴大题,解决此类问题,必须有过硬的数学基础知识与过人的数学技巧,同时运用数学归纳法也是比较好的选择,不过在使用数学归纳法的过程中,一定要遵循数学归纳法的步骤.