10.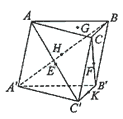 如图,在三棱柱ABC-A′B′C′中,点E、F、H、 K分
如图,在三棱柱ABC-A′B′C′中,点E、F、H、 K分
别为AC′、CB′、A′B、B′C′的中点,G为△ABC的
重心. 从K、H、G、B′中取一点作为P, 使得该棱柱恰有
2条棱与平面PEF平行,则P为 ( )
A.K B.H
C.G D.B′
解:用排除法.∵AB∥平面KEF,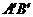 ∥平面KEF,
∥平面KEF,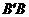 ∥平面KEF,
∥平面KEF, ∥平面KEF,否定(A),
∥平面KEF,否定(A),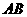 ∥平面HEF,
∥平面HEF,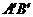 ∥平面HEF,
∥平面HEF, ∥平面HEF,
∥平面HEF, ∥平面HEF,否定(B),对于平面GEF,有且只有两条棱AB,
∥平面HEF,否定(B),对于平面GEF,有且只有两条棱AB,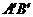 平面GEF,符合要求,故(C)为本题选择支.当P点选
平面GEF,符合要求,故(C)为本题选择支.当P点选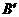 时有且只有一条棱AB∥平面PEF,综上选(C)
时有且只有一条棱AB∥平面PEF,综上选(C)
- 答案

