( 1 ) 若集合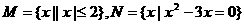 ,则M∩N
,则M∩N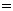 ( )
( )
A.{3} B.{0} C.{0,2} D.{0,3}
[答案]B
解: ∵由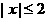 ,得
,得 ,
,
由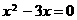 ,得
,得 ,
,
∴M∩N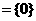 ,故选B.
,故选B.
( 2 ) 若 ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则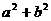 = ( )
= ( )
A.0 B.2 C.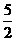 D.5
D.5
[答案]D
解: ∵  ,∴
,∴ ,
,
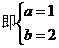 ,
,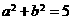 ,故选D.
,故选D.
( 3 ) 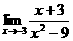 = ( )
= ( )
A.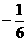 B.0 C.
B.0 C. D.
D.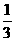
[答案]A
解: 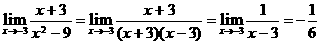 ,故选A.
,故选A.
 ( 4 ) 已知高为3的直棱锥
( 4 ) 已知高为3的直棱锥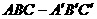 的底面是边长为1的正三角形
的底面是边长为1的正三角形
(如图1所示),则三棱锥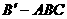 的体积为
( )
的体积为
( )
A. B.
B.
C.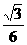 D.
D.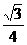
[答案]D
解:∵ 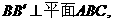
∴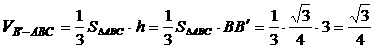 .
.
故选D.
( 5 ) 若焦点在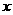 轴上的椭圆
轴上的椭圆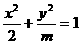 的离心率为
的离心率为 ,则m=( )
,则m=( )
A.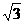 B.
B.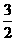 C.
C.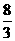 D.
D.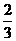
[答案]B
解: ∵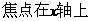 ,∴
,∴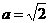 ,
,
∵
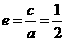 ,∴
,∴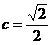 ,
,
∴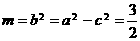 ,故选B.
,故选B.
( 6 )函数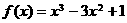 是减函数的区间为 ( )
是减函数的区间为 ( )
A.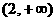 B.
B. C.
C. D.(0,2)
D.(0,2)
[答案]D
解: ∵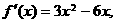
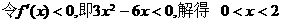 ,故选D.
,故选D.
( 7 ) 给出下列关于互不相同的直线 、
、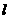 、
、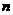 和平面
和平面 、
、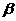 ,的四个命题:
,的四个命题:
①若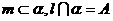 ,点
,点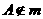 ,则
,则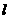 与
与 不共面;
不共面;
②若m、l是异面直线,  , 且
, 且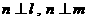 ,则
,则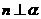 ;
;
③若 ,
, 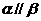 ,则
,则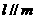 ;
;
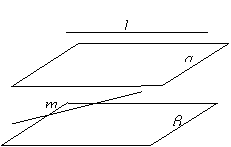 ④若
④若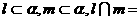 点
点 ,
,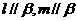 ,则
,则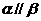 .
.
其中为假命题的是
A.① B.② C.③ D.④
[答案]C
解:③是假命题,如右图所示
满足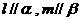 ,
, 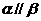 ,
,
但 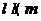 ,故选C.
,故选C.
( 8 ) 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子
朝上的面的点数分别为X、Y,则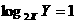 的概率为 ( )
的概率为 ( )
A. B.
B.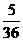 C.
C.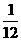 D.
D.
[答案]C
解:满足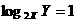 的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以
的X、Y有(1, 2),(2, 4),(3, 6)这3种情况,而总的可能数有36种,所以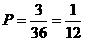 ,故选C.
,故选C.
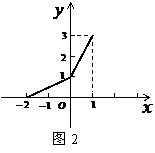
( 9 ) 在同一平面直角坐标系中,函数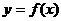 和
和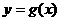 的图像
的图像
关于直线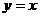 对称.现将
对称.现将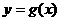 图像沿x轴向左平移2个单位,
图像沿x轴向左平移2个单位,
再沿y轴向上平移1个单位,所得的图像是由两条线段组成的折线
(如图2所示),则函数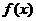 的表达式为
的表达式为
A.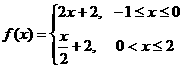 B.
B.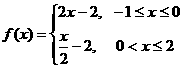
C.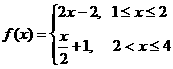 D.
D.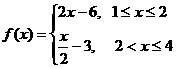
[答案]A
解:将图象沿y轴向下平移1个单位,再沿 轴向右平移2个单位得下图A,从而可以得到
轴向右平移2个单位得下图A,从而可以得到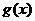 的图象,故
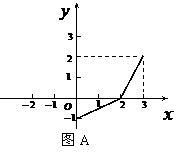
的图象,故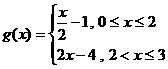 ,
,
 ∵函数
∵函数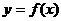 和
和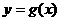 的图像关于直线
的图像关于直线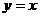 对称,
对称,
∴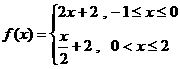 ,故选A.
,故选A.
(也可以用特殊点检验获得答案)
(10)已知数列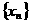 满足
满足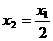 ,
,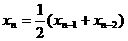 ,
,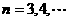 .若
.若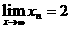 ,则
,则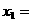
A.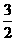 B.3 C.4 D.5
B.3 C.4 D.5
[答案]B
解法一:特殊值法,当 时,
时,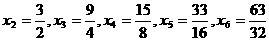
由此可推测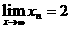 ,故选B.
,故选B.
解法二:∵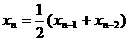 ,∴
,∴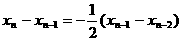 ,
,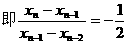 ,
,
∴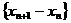 是以(
是以(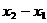 )为首项,以
)为首项,以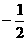 为公比6的等比数列,
为公比6的等比数列,
令 ,则
,则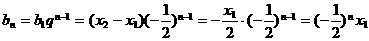
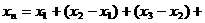 …
…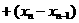
 …
…
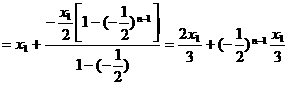
∴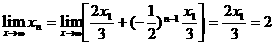 ,∴
,∴ ,故选B.
,故选B.
解法三:∵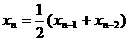 ,∴
,∴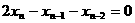 ,
,
∴其特征方程为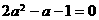 ,
,
解得 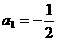 ,
,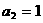 ,
,
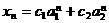 ,
,
∵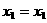 ,
,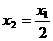 ,∴
,∴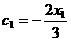 ,
,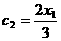 ,
,
∴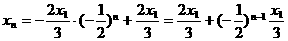 ,以下同解法二.
,以下同解法二.
- 答案

