19．(本小题满分12分)

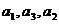　　　 已知{}是公比为q的等比数列，且成等差数列.

　 (Ⅰ)求q的值；

(Ⅱ)设{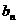}是以2为首项，q为公差的等差数列，其前n项和为S_n，当n≥2时，比较S_n与b_n的大小，并说明理由.

解：(Ⅰ)由题意得：2a₂=a₁+a₂,即2a₂q²=a₁+a₁q,,∵a₁≠0,∴2q²-q-1=0,∴q=1或q=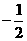

(Ⅱ)若q=1,则.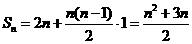

当n≥2时,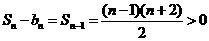,故

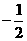若q=,则,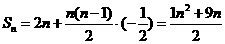

当n≥2时, ,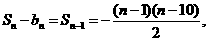

故对于n∈N⁺,当2≤n≤9时,S_n>b_n；当n=10时, S_n=b_n；当n≥11时, S_n<b_n