22.(本小题满分14分)
已知数列{an}满足a1=a,
an+1=1+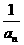 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
(Ⅰ)求当a为何值时a4=0;
(Ⅱ)设数列{bn}满足b1=-1, bn+1=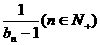 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(Ⅲ)若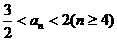 ,求a的取值范围.
,求a的取值范围.
解:(Ⅰ)∵a1=a,∴1+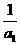 =a2,∴a2=
=a2,∴a2=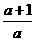 ,
, ,
,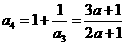 ,
,
故当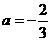 时,
时,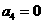
(Ⅱ)∵b1=-1,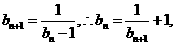
当a=b1时,a1=1+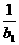 =0
=0
当a=b2时,a2=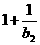 =b1,∴a2=0,
=b1,∴a2=0,
当a=b3时,a3=1+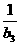 =b2,∴a3=1+
=b2,∴a3=1+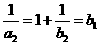 ,∴a4=0,
,∴a4=0,
……
一般地,当a=bn时,an+1=0,可得一个含育n+1项的有穷数列a1,a2,a3,…,an+1.
可用数学归纳法加以证明:
① 当n=1时,a=b1,显然a2=0,得到一个含2项的有穷数列a1,a2.
②
假设当n=k时,a=bk,得到一个含有k+1项的有穷数列a1,a2,a3,…,ak+1,其中ak+1=0,则n=k+1时.a=bk+1,∴a2=1+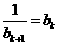 .
.
由假设可知,可得到一个含有k+1项的有穷数列a2,a3,…,ak+2,其中ak+2=0.
由①②知,对一切n∈N+,命题都成立.
(Ⅲ)要使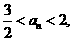 即
即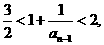 ,∴1<an-1<2.
,∴1<an-1<2.
∴要使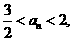 ,当且仅当它的前一项an-1,满足1<an-1<2,∵(
,当且仅当它的前一项an-1,满足1<an-1<2,∵(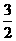 ,2)
,2)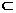 (1,2),
(1,2),
∴只须当a4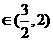 ,都有
,都有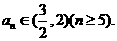
由 得
得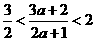 ,
,
解不等式组 得
得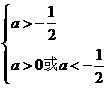 ,故a>0.
,故a>0.
- 答案

