19.(本小题满分12分)
已知函数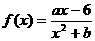 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
解:(Ⅰ)由函数f(x)的图象在点(-1,f(-1))处的切线方程为x+2y+5=0,知-1+2f(-1)+5=0,即f(-1)=-2,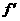 (-1)=
(-1)=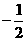 .∵
.∵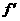 (x)=
(x)=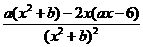 ,∴
,∴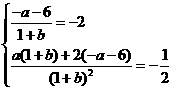
即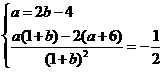 解得a=2,b=3(∵b+1≠0,∴b=-1舍去)
解得a=2,b=3(∵b+1≠0,∴b=-1舍去)
∴所求函数y=f(x)的解析式是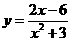
(Ⅱ)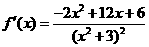 ,令-2x2+12x+6=0,解得x1=
,令-2x2+12x+6=0,解得x1=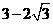 ,x2=
,x2=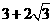
当x<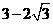 ,或x>
,或x>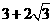 时,
时, ;当
;当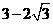 <x<时,
<x<时,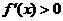 ,
,
所以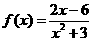 在(-∞,
在(-∞, 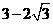 )内是减函数;在(
)内是减函数;在(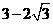 ,
,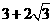 )内是增函数;
)内是增函数;
在(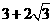 ,+∞)内是减函数
,+∞)内是减函数
- 答案

