17、解：(1)f(x)＝x³+ax²+bx+c，f¢(x)＝3x²+2ax+b

由f¢(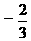)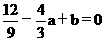＝，f¢(1)＝3+2a+b＝0得

a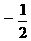＝，b＝－2

f¢(x)＝3x²－x－2＝(3x+2)(x－1)，函数f(x)的单调区间如下表：

x	(－¥，－)	－	(－，1)	1	(1，+¥)
f¢(x)	+	0	－	0	+
f(x)	­	极大值	¯	极小值	­

所以函数f(x)的递增区间是(－¥，－)与(1，+¥)

递减区间是(－，1)

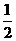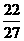(2)f(x)＝x³－x²－2x+c，xÎ(－1，2)，当x＝－时，f(x)＝+c

为极大值，而f(2)＝2+c，则f(2)＝2+c为最大值。

要使f(x)<c²(xÎ(－1，2))恒成立，只需c²>f(2)＝2+c

解得c<－1或c>2