20.本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力。
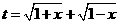
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴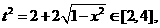 t≥0
①
t≥0
①
t的取值范围是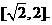 由①得
由①得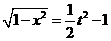
∴m(t)=a(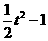 )+t=
)+t=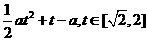
(2)由题意知g(a)即为函数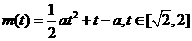 的最大值。
的最大值。
注意到直线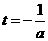 是抛物线
是抛物线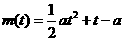 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
当a>0时,函数y=m(t), 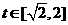 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由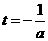 <0知m(t)在
<0知m(t)在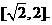 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 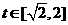 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 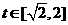 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若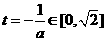 ,即
,即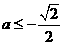 则
则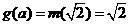
若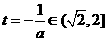 ,即
,即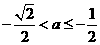 则
则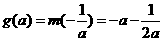
若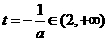 ,即
,即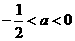 则
则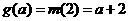
综上有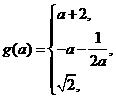
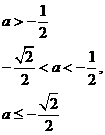
(3)解法一:
情形1:当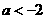 时
时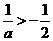 ,此时
,此时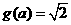 ,
,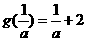
由 ,与a<-2矛盾。
,与a<-2矛盾。
情形2:当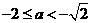
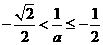 时,此时
时,此时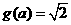 ,
,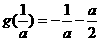
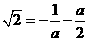 解得,
解得, 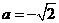 与
与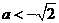 矛盾。
矛盾。
情形3:当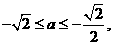
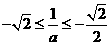 时,此时
时,此时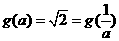
所以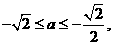
情形4:当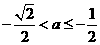 时,
时,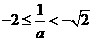 ,此时
,此时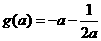 ,
,
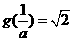
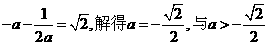 矛盾。
矛盾。
情形5:当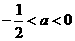 时,
时,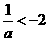 ,此时g(a)=a+2,
,此时g(a)=a+2,
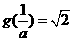
由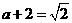 解得
解得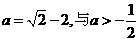 矛盾。
矛盾。
情形6:当a>0时,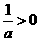 ,此时g(a)=a+2,
,此时g(a)=a+2, 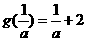
由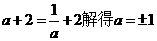 ,由a>0得a=1.
,由a>0得a=1.
综上知,满足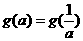 的所有实数a为
的所有实数a为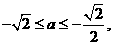 或a=1
或a=1
21本小题主要考查等差数列、充要条件等基础知识,考查综合运用数学知识分析问题、解决问题的能力。
证明:必要性,设是{an}公差为d1的等差数列,则
bn+1–bn=(an+1–an+3) – (an–an+2)= (an+1–an) – (an+3–an+2)= d1– d1=0
所以bn bn+1
( n=1,2,3,…)成立。
bn+1
( n=1,2,3,…)成立。
又cn+1–cn=(an+1–an)+2 (an+2–an+1)+3 (an+3–an+2)= d1+2 d1 +3d1 =6d1(常数) ( n=1,2,3,…)
所以数列{cn}为等差数列。
充分性:
设数列{cn}是公差为d2的等差数列,且bn bn+1
( n=1,2,3,…)
bn+1
( n=1,2,3,…)
∵cn=an+2an+1+3an+2 ①
∴cn+2=an+2+2an+3+3an+4 ②
①-②得cn–cn+2=(an–an+2)+2 (an+1–an+3)+3 (an+2–an+4)=bn+2bn+1+3bn+2
∵cn–cn+2=( cn–cn+1)+( cn+1–cn+2)= –2 d2
∴bn+2bn+1+3bn+2=–2 d2 ③
从而有bn+1+2bn+2+3bn+3=–2 d2 ④
④-③得(bn+1–bn)+2 (bn+2–bn+1)+3 (bn+3–bn+2)=0 ⑤
∵bn+1–bn≥0, bn+2–bn+1≥0 , bn+3–bn+2≥0,
∴由⑤得bn+1–bn=0 ( n=1,2,3,…),
由此不妨设bn=d3 ( n=1,2,3,…)则an–an+2= d3(常数).
由此cn=an+2an+1+3an+2= cn=4an+2an+1–3d3
从而cn+1=4an+1+2an+2–5d3 ,
两式相减得cn+1–cn=2( an+1–an) –2d3
因此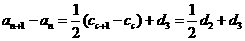 (常数) ( n=1,2,3,…)
(常数) ( n=1,2,3,…)
所以数列{an}公差等差数列。
[解后反思]理解公差d的涵义,能把文字叙述转化为符号关系式.利用递推关系是解决数列的重要方法,要求考生熟练掌握等差数列的定义、通项公式及其由来.
- 答案

