19. (本小题满分14分)已知函数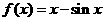 ,
,
数列{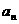 }满足:
}满足: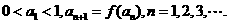
证明: (I).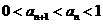 ;
;
(II).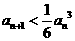 .
.
证明: (I).先用数学归纳法证明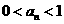 ,n=1,2,3,…
,n=1,2,3,…
(i).当n=1时,由已知显然结论成立.
(ii).假设当n=k时结论成立,即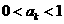 .因为0<x<1时
.因为0<x<1时
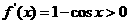 ,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
从而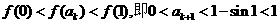 .故n=k+1时,结论成立.
.故n=k+1时,结论成立.
由(i)、(ii)可知,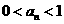 对一切正整数都成立.
对一切正整数都成立.
又因为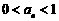 时,
时,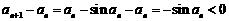 ,
,
所以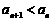 ,综上所述
,综上所述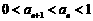 .
.
(II).设函数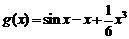 ,
,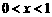 .由(I)知,当
.由(I)知,当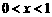 时,
时,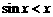 ,
,
从而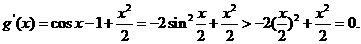
所以g (x)在(0,1)上是增函数. 又g (x)在[0,1]上连续,且g (0)=0,
所以当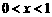 时,g (x)>0成立.于是
时,g (x)>0成立.于是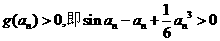 .
.
故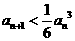 .
.
- 答案

