20.(本小题满分14分)
设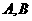 分别为椭圆
分别为椭圆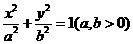 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且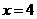 为它的右准线。
为它的右准线。
(Ⅰ)、求椭圆的方程;
(Ⅱ)、设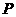 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线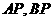 分别与椭圆相交于异于
分别与椭圆相交于异于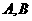 的点
的点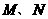 ,证明点
,证明点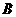 在以
在以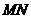 为直径的圆内。
为直径的圆内。
(此题不要求在答题卡上画图)
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力。
解:(Ⅰ)依题意得 a=2c,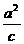 =4,解得a=2,c=1,从而b=
=4,解得a=2,c=1,从而b=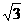 .
.
故椭圆的方程为 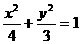 .
.
(Ⅱ)解法1:由(Ⅰ)得A(-2,0),B(2,0).设M(x0,y0).
∵M点在椭圆上,∴y0=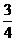 (4-x02).
1
(4-x02).
1
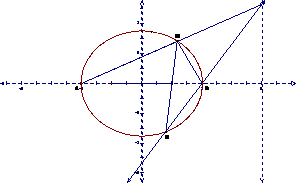 又点M异于顶点A、B,∴-2<x0<2,由P、A、M三点共线可以得
又点M异于顶点A、B,∴-2<x0<2,由P、A、M三点共线可以得
P(4,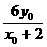 ).
).
从而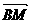 =(x0-2,y0),
=(x0-2,y0),
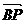 =(2,
=(2,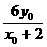 ).
).
∴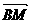 ·
·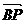 =2x0-4+
=2x0-4+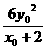 =
=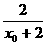 (x02-4+3y02). 2
(x02-4+3y02). 2
将1代入2,化简得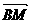 ·
·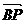 =
=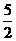 (2-x0).
(2-x0).
∵2-x0>0,∴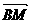 ·
·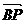 >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内。
解法2:由(Ⅰ)得A(-2,0),B(2,0).设M(x1,y1),N(x2,y2),
则-2<x1<2,-2<x2<2,又MN的中点Q的坐标为( ,
,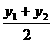 ),
),
依题意,计算点B到圆心Q的距离与半径的差
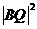 -
-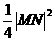 =(
=( -2)2+(
-2)2+(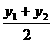 )2-
)2-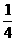 [(x1-x2)2+(y1-y2)2]
[(x1-x2)2+(y1-y2)2]
=(x1-2) (x2-2)+y1y1 3
又直线AP的方程为y=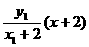 ,直线BP的方程为y=
,直线BP的方程为y=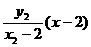 ,
,
而点两直线AP与BP的交点P在准线x=4上,
∴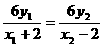 ,即y2=
,即y2= 4
4
又点M在椭圆上,则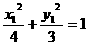 ,即
,即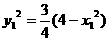 5
5
于是将4、5代入3,化简后可得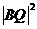 -
-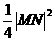 =
=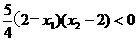 .
.
从而,点B在以MN为直径的圆内。
- 答案

