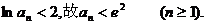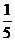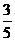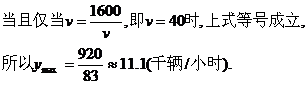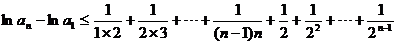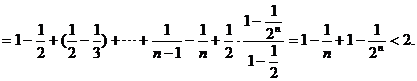1函数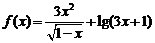 的定义域是
的定义域是
A.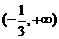 B.
B. 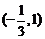 C.
C.
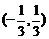 D.
D. 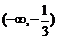
2随机变量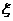 的的分布列如下,则m=
的的分布列如下,则m=
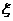
1
2
3
4
p
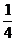
m
A 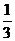 B
B  C
C 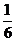 D
D 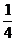
3在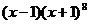 的展开式中
的展开式中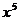 的系数是
的系数是
A.-14 B.
4已知双曲线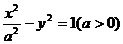 的一条准线为
的一条准线为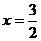 ,则该双曲线的离心率为
,则该双曲线的离心率为
A.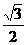 B.
B.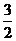 C.
C.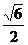 D.
D.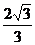
5设直线l过点(-2,0),且与圆x2+y2=1相切,则l的斜率是
A.±1 B.± C.±
C.±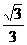 D.±
D.±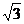
6设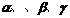 为平面,
为平面,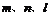 为直线,则
为直线,则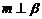 的一个充分条件是
的一个充分条件是
A. 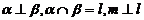 B.
B.
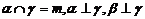
C. 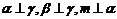 D.
D.
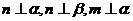
7某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为
A. B.
B.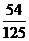 C.
C.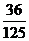 D.
D.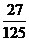
8 如果数列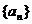 是等差数列,则
是等差数列,则
A.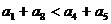 B.
B.
C.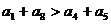 D.
D.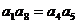
9 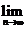
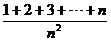 =
=
A. 2
B. D.0
D.0
10已知向量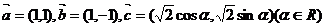 ,实数m,n满足
,实数m,n满足
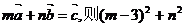 的最大值为
的最大值为
A.2 B.
11不共面的四个定点到平面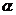 的距离都相等,这样的平面
的距离都相等,这样的平面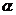 共有
共有
A.3个 B.4个 C.6个 D.7个
12设函数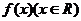 为奇函数,
为奇函数,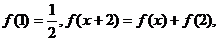 则
则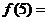
A.0 B.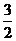 C.
C.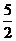 D.
D.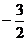
13、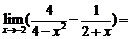 ________.
________.
14、棱长为3的正方体的顶点都在同一球面上,则该球的表面积为________.
15某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆。为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取 ,z , 辆。
16设函数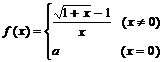 在
在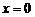 处连续,则实数
处连续,则实数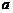 的值为
.
的值为
.
 江西省大余中学2006―2007学年度高三数学考试答案卷
江西省大余中学2006―2007学年度高三数学考试答案卷
2006年9月
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
13. 14. 15. 16.
17(12分)从4名男生和2名女生中任选3人参加演讲比赛,设随机变量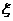 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求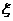 的分布列;
的分布列;
(Ⅱ)求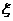 的数学期望;
的数学期望;
18(12分)数列an=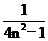 ,它的前n项和为Sn,求
,它的前n项和为Sn,求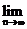 Sn
Sn
 19(12分)如图,在底面为平行四边表的四棱锥
19(12分)如图,在底面为平行四边表的四棱锥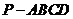 中,
中,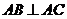 ,
,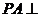 平面
平面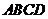 ,且
,且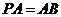 ,点
,点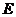 是
是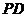 的中点.
的中点.
(Ⅰ)求证: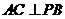 ;
;
(Ⅱ)求证: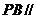 平面
平面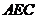 ;
;
(Ⅲ)求二面角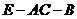 的大小.
的大小.
20(12分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量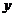 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度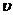 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: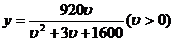 .
.
(1)在该时段内,当汽车的平均速度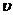 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
21(12分)已知椭圆中心在原点,焦点在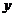 轴上,焦距为4,离心率为
轴上,焦距为4,离心率为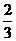 ,
,
(Ⅰ)求椭圆方程;
(Ⅱ)设椭圆在y轴正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段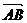 所成的比为2,求线段AB所在直线的方程。
所成的比为2,求线段AB所在直线的方程。
22(14分)数列{an}满足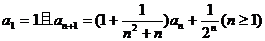 .
.
(Ⅰ)用数学归纳法证明: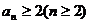 ;
;
(Ⅱ)已知不等式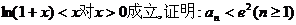 ,其中无理数
,其中无理数
e=2.71828….
答案:一、BDBD CDAB CDDC
二、(13 )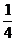 (14
) 27π ( 15 ) 6,30 ,10 ( 17)
(14
) 27π ( 15 ) 6,30 ,10 ( 17)
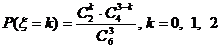 。所以,
。所以,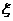 的分布列为
的分布列为
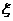
0
1
2
P
(Ⅱ)解:由(1),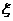 的数学期望为
的数学期望为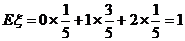
18解: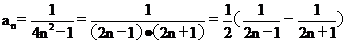
Sn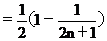
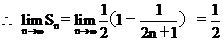
19(Ⅰ)略;(Ⅱ)略;(Ⅲ) 。
。
20解:(Ⅰ)依题意,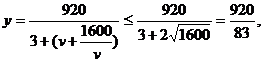
(Ⅱ)由条件得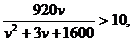 整理得v2-89v+1600<0, ,解得25<v<64.
整理得v2-89v+1600<0, ,解得25<v<64.
21解:(Ⅰ) 所求的椭圆方程为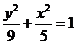
(Ⅱ)若k 不存在,则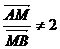 ,若k 存在,则设直线AB的方程为:y=kx+2
,若k 存在,则设直线AB的方程为:y=kx+2
又设A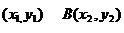
由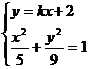 得
得 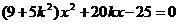
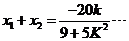 ①
①
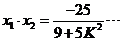 ②
②
∵点M坐标为M(0,2) ∴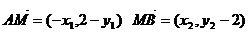
由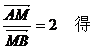
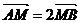 ∴
∴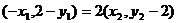
∴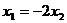 代入①、②得
代入①、②得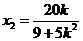 … ③
… ③ 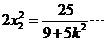 ④
④
由③、④ 得 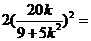
 ∴
∴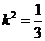
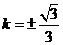
∴线段AB所在直线的方程为: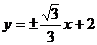 。
。
22证明:(1)当n=2时,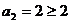 ,不等式成立. (2)假设当
,不等式成立. (2)假设当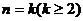 时不等式成立,即
时不等式成立,即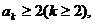 那么
那么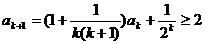 . 这就是说,当
. 这就是说,当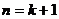 时不等式成立.
时不等式成立.
根据(1)、(2)可知: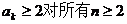 成立.
成立.
(Ⅱ)由递推公式及(Ⅰ)的结论有 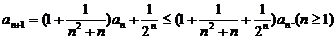
两边取对数并利用已知不等式得 
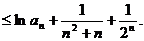 故
故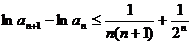
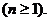
上式从1到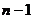 求和可得
求和可得
即