1.已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x²+x－6≤0}, 则P∩Q等于(  )

  A. {2}     B.{1,2}   C.{2,3}  D.{1,2,3}

2.复数等于(    )

 A.1－i     B.1+i     C.－1+ i     D.－1－i

3. n→∞lim等于(   )

 A. 1    B.      C.     D.0

4.设函数f(x)=log_a(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于(   )

A.6           B.5    C.4      D.3

5.设直线过点(0,a),其斜率为1, 且与圆x²+y²=2相切,则a 的值为(   )

A.±    B.±2      B.±2    D.±4

6."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的(  )

A.必要而不充分条件    B.充分而不必要条件

C.充分必要条件        D.既不充分又不必要条件

7.已知双曲线 － =1(a>)的两条渐近线的夹角为,则双曲线的离心率为(  )

A.2        B.     C.       D.

8.已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为(   )

A.2   B.4     C.6     D.8

9.已知非零向量与满足(+)・=0且・= , 则△ABC为(  )

A.三边均不相等的三角形    B.直角三角形

C.等腰非等边三角形        D.等边三角形

10.已知函数f(x)=ax²+2ax+4(0<a<3),若x₁<x₂,x₁+x₂=1－a,则(    )

A.f(x₁)<f(x₂)     B.f(x₁)=f(x₂)    C.f(x₁)>f(x₂)   D.f(x₁)与f(x₂)的大小不能确定

11.已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是(   )

A.平面ABC必平行于α      B.平面ABC必与α相交

C.平面ABC必不垂直于α    D.存在△ABC的一条中位线平行于α或在α内

12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为(  )

A.4,6,1,7   B.7,6,1,4      C.6,4,1,7    D.1,6,4,7

第二部分（共90分）

13.cos43°cos77°+sin43°cos167°的值为     

14.(3x－)¹²展开式x^－3的系数为        (用数字作答)

15.水平桌面α上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球,它和下面4个球恰好都相切,则小球的球心到水平桌面α的距离是         

16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有      种

17.(本小题满分12分)

已知函数f(x)=sin(2x－)+2sin²(x－) (x∈R)

(Ⅰ)求函数f(x)的最小正周期    ;  (2)求使函数f(x)取得最大值的x的集合.

18. (本小题满分12分)

甲、乙、丙3人投篮,投进的概率分别是, , .

(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;

(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.

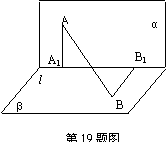
19. (本小题满分12分)

如图,α⊥β,α∩β=l , A∈α, B∈β,点A在直线l 上的射影为A₁, 点B在l的射影为B₁,已知AB=2,AA₁=1, BB₁=, 求:

 (Ⅰ) 直线AB分别与平面α,β所成角的大小; (Ⅱ)二面角A₁－AB－B₁的大小.

20. (本小题满分12分)

 已知正项数列{a_n}，其前n项和S_n满足10S_n=a_n²+5a_n+6且a₁,a₃,a₁₅成等比数列，求数列{a_n}的通项a_n .

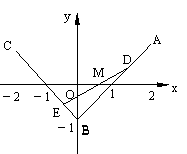
21. (本小题满分12分)

如图,三定点A(2,1),B(0,－1),C(－2,1); 三动点D,E,M满足=t,  = t , =t , t∈[0,1]. (Ⅰ) 求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程.

22.（本小题满分１4分）

已知函数f(x)=x³－x²+ + , 且存在x₀∈(0, ) ,使f(x₀)=x₀.

（I）证明：f(x)是R上的单调增函数；设x₁=0, x_n+1=f(x_n);       y₁=, y_n+1=f(y_n),

其中　n=1,2,……

（II）证明：x_n<x_n+1<x₀<y_n+1<y_n;

（III）证明： <   .