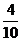1.设全集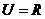 ,集合
,集合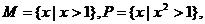 则下列关系中正确的是
则下列关系中正确的是
A.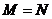 B.
B.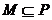 C.
C.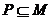 D.
D.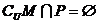
2.若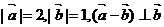 ,则
,则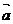 与
与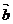 的夹角是
的夹角是
A.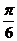 B.
B.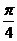 C.
C.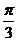 D.
D.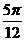
3.若命题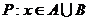 ,则
,则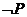 是
是
A.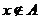 且
且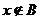 B.
B.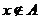 或
或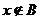
C.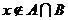 D.
D.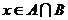
4.把函数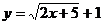 的图象按向量
的图象按向量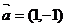 平移,则所得图象的函数解析式为
平移,则所得图象的函数解析式为
A.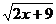 B.
B.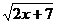 C.
C.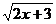 D.
D.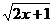
5.二项展开式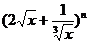 的各项系数之和为
的各项系数之和为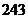 ,则展开式中的常数项为
,则展开式中的常数项为
A.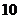 B.
B.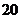 C.
C. D.
D.
6.在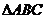 中,
中,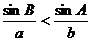 是
是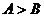 成立的
成立的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
7.若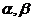 是两个相交平面,点
是两个相交平面,点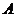 不在
不在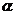 内,也不在
内,也不在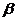 内,则过点
内,则过点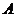 且与
且与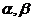 都平行的直线
都平行的直线
A.只有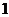 条 B.只有
条 B.只有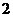 条 C.只有
条 C.只有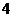 条 D.有无数条
条 D.有无数条
8.一名同学投篮的命中率为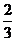 ,他连续投篮3次,其中恰有2次命中的概率是
,他连续投篮3次,其中恰有2次命中的概率是
A.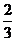 B.
B.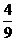 C.
C.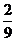 D.
D.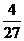
9.设函数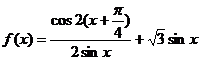 ,则当
,则当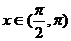 时,函数
时,函数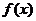 的值域是
的值域是
A.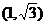 B.
B.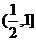 C.
C.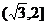 D.
D.
10.用四种不同的颜色给正方体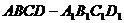 的六个面染色,要求相邻两个面涂不同的颜色,且四种颜色均用完,则所有不同的涂色方法共有
的六个面染色,要求相邻两个面涂不同的颜色,且四种颜色均用完,则所有不同的涂色方法共有
A.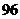 种 B.
种 B. 种 C.
种 C.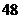 种 D.
种 D. 种
种
第Ⅱ卷(共100分)
11.在等比数列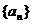 中,
中,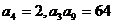 ,则
,则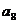 等于
.
等于
.
12.若椭圆的焦点到其相应准线的距离等于半焦距长,则椭圆的离心率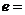 .
.
13.在抽查某产品的尺寸过程中,将其尺寸分成若干组,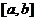 是其中的一组,抽查出的个体数在该组上的频率为
是其中的一组,抽查出的个体数在该组上的频率为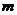 ,该组上的直方图的高为
,该组上的直方图的高为 ,则
,则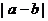 等于 .
等于 .
14.已知球面上三点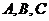 ,且
,且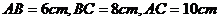 ,球的半径为
,球的半径为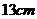 ,则球心到平面
,则球心到平面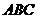 的距离为
的距离为
 .
.
15.已知函数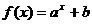 的图象过点
的图象过点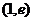 ,其反函数
,其反函数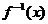 的图象过点
的图象过点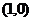 ,则
,则
(1)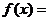 ;
;
(2)若方程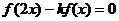 没有实根,则实数
没有实根,则实数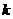 的取值范围是
.
的取值范围是
.
16.(本小题满分12分)
已知5条桥梁横跨A、B两岸,假设各条桥梁的车流量分别为1、1、2、2、3(单
位:万量),现从这5条桥梁中任取三条桥梁,考察这三条桥梁的车流量之和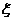 .
.
(1)求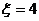 的概率;
的概率;
(2)求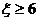 的概率.
的概率.
17.(本小题满分12分)
平面直角坐标系中,已知点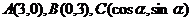 .
.
(1)若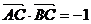 ,求
,求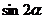 的值;
的值;
(2)若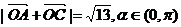 ,求
,求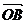 与
与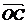 的夹角.
的夹角.
18.(本小题满分14分)
 如图,在正三棱柱
如图,在正三棱柱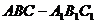 中,
中,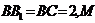
是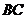 中点,点
中点,点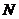 在
在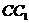 上.
上.
(1)试确定点N的位置,使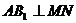 ;
;
(2)当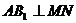 时,求二面角
时,求二面角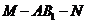 的大小.
的大小.
19.(本小题满分14分)
以数列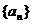 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点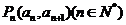 均在一次函数
均在一次函数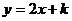 的图象上,数列
的图象上,数列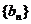 满足条件:
满足条件: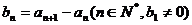 .
.
(1)求证:数列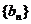 是等比数列;
是等比数列;
(2)设数列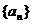 ,
,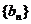 前
前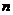 项和分别为
项和分别为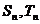 ,若
,若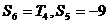 ,求
,求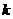 的值.
的值.
20.(本小题满分14分)
某种商品在 天内每件的销售价格
天内每件的销售价格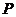 (元)与时间
(元)与时间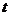
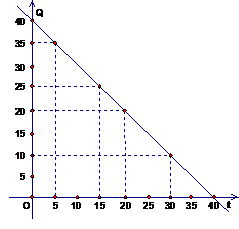
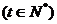 (天)的函数关系用右图的两条线段表示,该商品在
(天)的函数关系用右图的两条线段表示,该商品在 内日销售量
内日销售量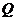 (件)与时间
(件)与时间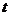
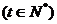 (天)之间的关系如下表:
(天)之间的关系如下表:
第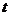 天
天
5
15
20
30
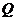 件
件
35
25
20
10
 (1)根据提供的图象,写出该商品每件
(1)根据提供的图象,写出该商品每件
的销售价格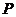 与时间
与时间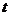 的函数关系;
的函数关系;
(2)在所给直角坐标系中,根据表中提
供的数据描出实数对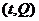 的对应点,并
的对应点,并
确定日销售量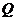 与时间
与时间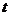 的一个函数关系
的一个函数关系
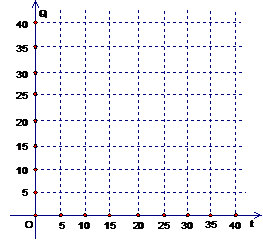 式;
式;
(3)求该商品的日销售金额的最大值,
并指出日销售金额最大的一天是 天中
天中
的第几天?(日销售金额=每件的销售价
格 日销售梁)
日销售梁)
21.(本小题满分14分)
已知: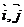 分别是
分别是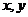 轴正方向上的两个单位向量,
轴正方向上的两个单位向量,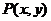 是直角平面上的一个动点,
是直角平面上的一个动点,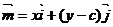 ,
,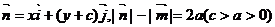 ,设动点P的曲线方程为C,点
,设动点P的曲线方程为C,点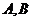 是曲线C上位于第一象限的不同两点.
是曲线C上位于第一象限的不同两点.
(1)求曲线C的方程;
(2)设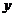 轴上一点T满足条件:
轴上一点T满足条件: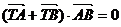 ,求
,求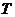 点的纵坐标的取值范围.
点的纵坐标的取值范围.
雅礼中学2006届高三第一次模拟考试
数学试卷(文史类)答案
1.B 2.C 3.A 4.C 5.D
6.C 7.A 8.B 9.D 10.B
11.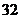 12.
12.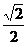 13.
13.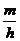 14.
14.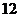 15.(1)
15.(1)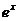 ;(2)
;(2)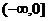
16.(本小题满分12分)
解:(1)由等可能事件得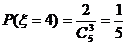 .……………………………………… 5分
.……………………………………… 5分
(2)由已知得:
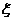
6
7
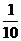
……………………………………………………………………………………………10分
故由互斥事件得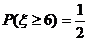 . ……………………………………………………12分
. ……………………………………………………12分
17.(本小题满分12分)
解:(1)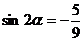 . ……………………………………………………………… 6分
. ……………………………………………………………… 6分
(2)由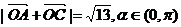 得
得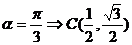 . …………………10分
. …………………10分
由夹角公式得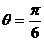 . …………………………………………………………………12分
. …………………………………………………………………12分
18.(本小题满分14分)
解:(1)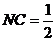 . ……………………………………………………………… 6分
. ……………………………………………………………… 6分
(2)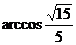 . ………………………………………………………………14分
. ………………………………………………………………14分
19.(本小题满分14分)
解:(1)(略) ……………………………………………………………………………… 6分
(2)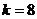 . ……………………………………………………………………………14分
. ……………………………………………………………………………14分
20.(本小题满分14分)
 解:(1)由已知得:
解:(1)由已知得:
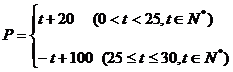 .…4分
.…4分
(2)如图所示,对应的一个函数关系式为
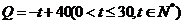 . …… 8分
. …… 8分
(3)分段函数分段处理得
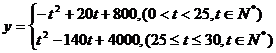 , ………………………………………11分
, ………………………………………11分
当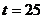 时,日销售金额最大,且最大值为
时,日销售金额最大,且最大值为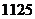 元. ……………………………14分
元. ……………………………14分
21.(本小题满分14分)
解:(1)由双曲线的定义得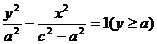 . ……………………………… 6分
. ……………………………… 6分
(2)由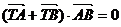 得
得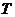 即为线段
即为线段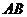 的中垂线与
的中垂线与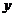 轴的交点.………… 8分
轴的交点.………… 8分
令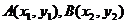 ,则线段
,则线段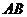 的中垂线方程为
的中垂线方程为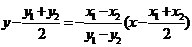 ,
,
所以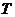 的纵坐标为
的纵坐标为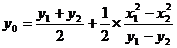 . …………………………………10分
. …………………………………10分
由点差法得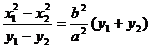 , ………………………………………………12分
, ………………………………………………12分
代入得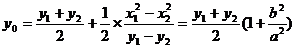 .
.
又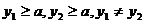 ,则
,则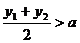 , ……………………………………13分
, ……………………………………13分
所以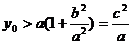 ,即
,即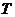 点的纵坐标的取值范围是
点的纵坐标的取值范围是 . …………14分
. …………14分