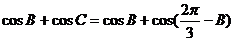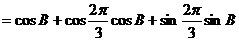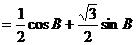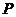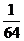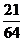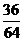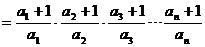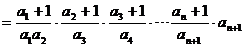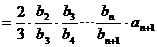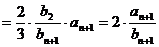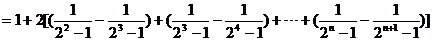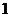 .计算
.计算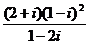 =( )
=( )
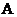 .
.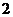
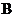 .
.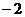
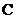 .
.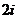
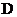 .
.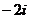
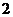 .若
.若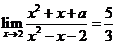 ,则
,则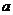 的值是( )
的值是( )
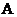 .
.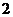
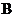 .
.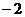
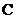 .
.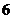
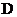 .
.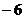
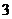 .在
.在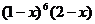 的展开式中,
的展开式中,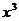 的系数是( )
的系数是( )
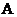 .
.
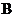 .
.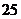
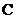 .
.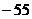
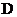 .
.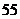
 .已知向量
.已知向量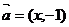 与向量
与向量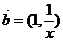 ,则不等式
,则不等式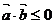 的解集为( )
的解集为( )
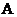 .
.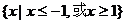
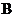 .
.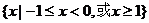
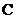 .
.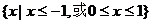
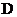 .
.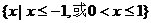
 .已知
.已知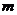 、
、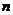 为两条不同的直线,
为两条不同的直线,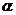 、
、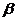 为两个不同的平面,且
为两个不同的平面,且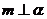 ,
,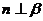 ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
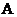 .若
.若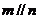 ,则
,则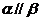
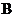 .若
.若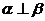 ,则
,则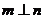
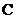 .若
.若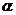 ,
,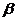 相交,则
相交,则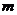 ,
,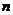 也相交
也相交 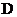 .若
.若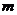 ,
,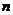 相交,则
相交,则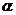 ,
,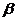 也相交
也相交
 .已知函数
.已知函数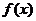 的图像如图所示,
的图像如图所示,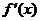 是函数
是函数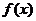 的导函数,且
的导函数,且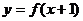 是奇函数,则下列结论中错误的是( )
是奇函数,则下列结论中错误的是( )
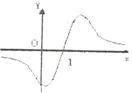
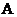 .
.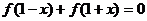
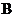 .
.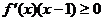
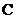 .
.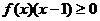
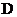 .
.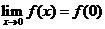
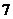 .函数
.函数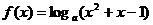 在区间
在区间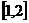 上的最大值比最小值大2,则
上的最大值比最小值大2,则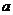 的值为( )
的值为( )
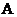 .
.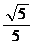
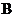 .
.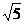
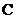 .
.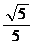 或
或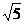
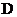 .不能确定
.不能确定
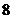 .锐角
.锐角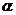 满足,
满足,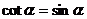 ,则
,则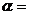 ( )
( )
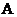 .
.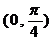
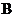 .
.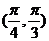
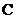 .
.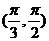
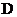 .
.
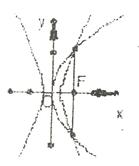
 .如图,已知抛物线
.如图,已知抛物线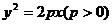 的焦点恰好是双曲线
的焦点恰好是双曲线
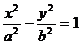 的右焦点,且两条曲线交点的连线过F,则该
的右焦点,且两条曲线交点的连线过F,则该
双曲线的离心率( )
 .
.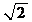
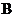 .
.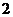
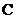 .
.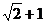
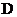 .
.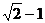
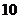 .数列
.数列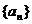 中,
中,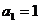 ,
,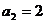 ,当
,当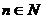 时,
时,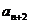 等于
等于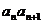 的个位数,若数列
的个位数,若数列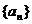 前
前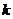 项和为243,则
项和为243,则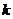 =( )
=( )
 .
.
 .
.
 .
.
 .
.
 .如图
.如图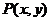 是边长为1的正方形内的一点,若
是边长为1的正方形内的一点,若
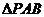 ,
,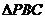 ,
,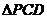 ,
,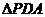 面积均不小于
面积均不小于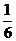 ,
,
则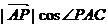 的最大值为( )
的最大值为( )
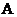 .
.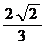
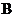 .
.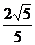
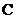 .
.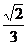
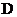 .
.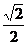
 .将4个相同的红球和4个相同的蓝球排成一排,从左到右每个球依次对应序号为1,2,8,若同色球之间不加区分,则4个红球对应序号之和小于4个蓝球对应序号之和的排列方法种数为( )
.将4个相同的红球和4个相同的蓝球排成一排,从左到右每个球依次对应序号为1,2,8,若同色球之间不加区分,则4个红球对应序号之和小于4个蓝球对应序号之和的排列方法种数为( )
 .
.
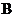 .
.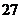
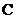 .
.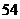
 .
.
江西省重点中学协作体09届高三第一次联考
理 科 数 学 试 题
第Ⅱ卷(非选择题,共90分)
请将选择题答案填入下表
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
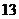 .已知在等差数列
.已知在等差数列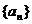 中,
中,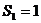 ,
,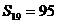 ,则
,则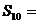 。
。
 .如图,在平面斜坐标系
.如图,在平面斜坐标系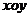 中,
中,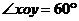 ,平面
,平面
上任一点P在斜坐标系中的斜坐标是这样定义的:若
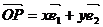 (
(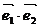 分别为
分别为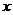 轴,
轴,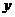 轴方向相同
轴方向相同
的单位向量)。则P点的斜坐标为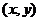 ,若点P满足
,若点P满足
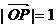 。则点P在斜坐标
。则点P在斜坐标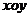 系中的轨迹方程
系中的轨迹方程
 是
。
是
。
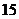 .过正四面体外接球球心的平面截正四面体所得截面如
.过正四面体外接球球心的平面截正四面体所得截面如
图所示,图中三角形面积为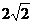 ,则正四面体棱长
,则正四面体棱长
为 。
 .关于曲线C:
.关于曲线C: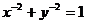 的下列说法:(1)关于原
的下列说法:(1)关于原
点对称;(2)是封闭图形,面积大于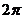 ;(3)不是封闭图形,与⊙O:
;(3)不是封闭图形,与⊙O: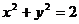 无公共点;(4)与曲线D:
无公共点;(4)与曲线D: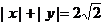 的四个交点恰为正方形的四个顶点,其中正确的序号是
。
的四个交点恰为正方形的四个顶点,其中正确的序号是
。
 .(本小题满分12分)已知锐角三角形
.(本小题满分12分)已知锐角三角形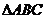 内角A、B、C对应边分别为a,b,c。
内角A、B、C对应边分别为a,b,c。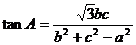
(Ⅰ)求A的大小;
(Ⅱ)求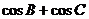 的取值范围。
的取值范围。
 .(本小题满分12分)某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立。又知电梯只在有人下时才停下,
.(本小题满分12分)某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立。又知电梯只在有人下时才停下,
(I)求某乘客在第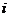 层下电梯的概率
层下电梯的概率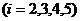 ;(Ⅱ)求电梯在第2层停下的概率;
;(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数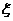 的数学期望。
的数学期望。
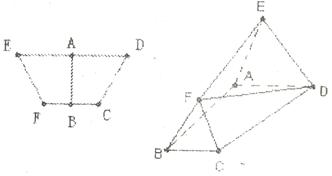
 .(本小题满分12分)等腰梯形EDCF中,A、B分别为DE、CF的中点,
.(本小题满分12分)等腰梯形EDCF中,A、B分别为DE、CF的中点,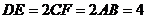 。沿AB将梯形折成60°的二面角。如图所示
。沿AB将梯形折成60°的二面角。如图所示
(Ⅰ)DF与平面ABCD所成角;
(Ⅱ)求二面角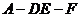 的大小。
的大小。
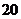 .(本小题满分12分)已知
.(本小题满分12分)已知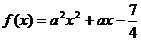 与
与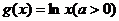
(Ⅰ)若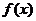 与
与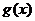 有公共点且在公共点处有相同的切线,试求
有公共点且在公共点处有相同的切线,试求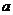 ;
;
(Ⅱ)在区间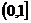 上,存在实数
上,存在实数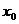 ,使
,使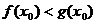 ,试求
,试求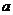 的取值范围。
的取值范围。
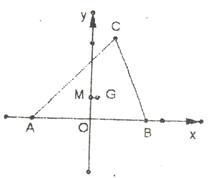
 .(本小题满分12分)设G、M分别为
.(本小题满分12分)设G、M分别为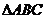 的重心和外心,
的重心和外心,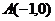 ,
,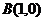 且
且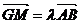
(Ⅰ)求点C的轨迹E的方程。
 (Ⅱ)设轨迹E与
(Ⅱ)设轨迹E与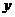 轴两个交点分别为
轴两个交点分别为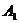 ,
,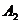 (
(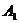 位于
位于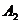 下方)。动点M、N均在轨迹E上,且满足
下方)。动点M、N均在轨迹E上,且满足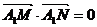 ,直线
,直线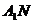 和
和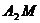 交点P是否恒在某条定直线
交点P是否恒在某条定直线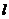 上,若是,试求出
上,若是,试求出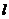 的方程;若不是,请说明理由。
的方程;若不是,请说明理由。
 .(本小题满分14分)数列
.(本小题满分14分)数列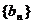 满足
满足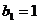 ,
,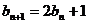 ,若数列
,若数列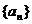 满足
满足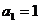 ,
,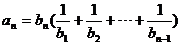
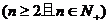
(Ⅰ)求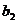 ,
,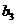 ,
,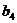 及
及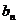 ; (Ⅱ)证明:
; (Ⅱ)证明: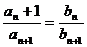
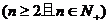
(Ⅲ)求证: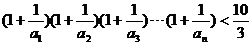
江西省重点中学协作体09届高三第一次联考
理 科 数 学 试 题 答 案
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
D
C
D
C
B
C
B
C
B
A
A
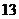 .
.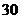
 .
.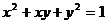
 .2
.2  .(1)(3)(4)
.(1)(3)(4)
 .(Ⅰ)由余弦定理知,
.(Ⅰ)由余弦定理知,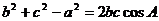 ……………………………3分
……………………………3分
∴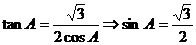
∵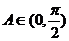
∴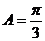 ……………………………6分
……………………………6分
(Ⅱ)∵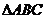 为锐角三角形且
为锐角三角形且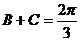
∴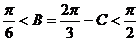 ……………………………7分
……………………………7分
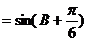 …………………………10分
…………………………10分
∵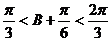
∴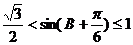
即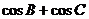 的取值范围是
的取值范围是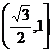 ……………………………12分
……………………………12分
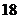 .解:(Ⅰ)
.解:(Ⅰ)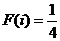 ;………3分 (Ⅱ)
;………3分 (Ⅱ)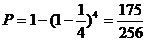 ………7分
………7分
(Ⅲ)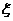 可取1、2、3、4四种值
可取1、2、3、4四种值
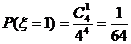 ;
; 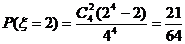 ;
;
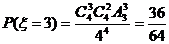 ;
;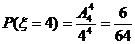
故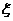 的分别列如下表:
的分别列如下表:
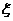
1
2
3
4
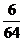
……………………12分
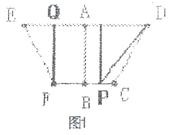 ∴
∴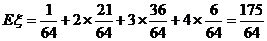 ……………………12分
……………………12分
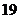 .解:如图所示,易知图(1)中,
.解:如图所示,易知图(1)中,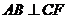 ,
,
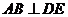 经折叠后,
经折叠后,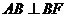 ,
,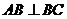
且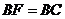
∴平面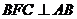 ∴平面
∴平面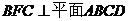 。
。
∵二面角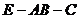 的大小为60°
∴
的大小为60°
∴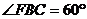
∴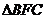 为等边三角形.
为等边三角形.
同理,平面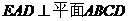
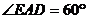
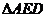 为等边三角形.
为等边三角形.
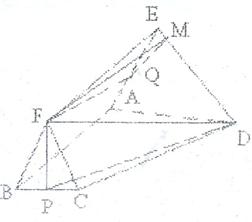 (Ⅰ)取BC的中点P,连接FP. ∵
(Ⅰ)取BC的中点P,连接FP. ∵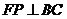
∴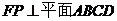 .
.
∴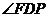 为DF与平面ABCD所成的角.
为DF与平面ABCD所成的角.
∵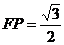 如图(1),
如图(1),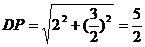
∴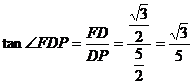 ,
,
故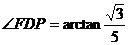 …………………6分
…………………6分
(Ⅱ)∵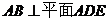
∴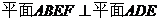 .
.
取AE的中点Q,连结FQ,则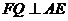 .
.
∴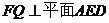 .
.
又作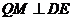 ,则由三垂线定理,
,则由三垂线定理,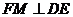 .
.
∴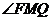 为二面角
为二面角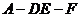 的平面角.
的平面角.
∵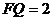 ,
,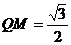 .
.
∴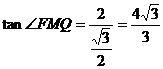 ,故
,故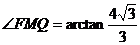 .
.
∴二面角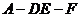 大小为
大小为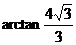 ………………12分
………………12分
法2(向量法)
如图所示建立空间直角坐标系O为BC的中点
易知各点坐标如下: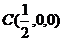 ,
,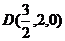 ,
,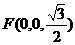
 又
又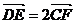 ∴E的坐标为
∴E的坐标为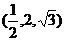
(Ⅰ)显然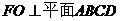
∴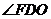 为DF与平面ABCD所成的角.
为DF与平面ABCD所成的角.
∴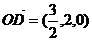 ,
,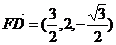
∴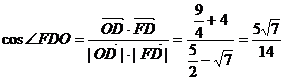 .
.
故DF与平面ABCD所成角的大小为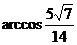 ……………6分
……………6分
(Ⅱ)设二面角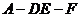 大小为
大小为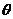 ,平面CDEF的法向量为
,平面CDEF的法向量为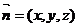
∵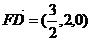 ,
,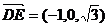
∴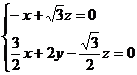
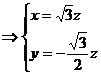 , 令
, 令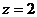 ,则
,则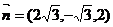
而平面ADE的法向量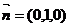 .
.
∴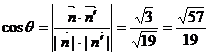
∴二面角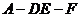 的大小为
的大小为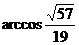 ……………12分
……………12分
 .解:(Ⅰ)依题意:设
.解:(Ⅰ)依题意:设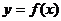 与
与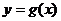 的公共点为
的公共点为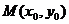
则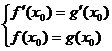
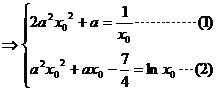 ……………3分
……………3分
由(1)得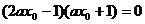 . ∵
. ∵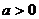
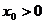 ∴
∴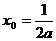
代入(2)式得: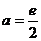 . ……………6分
. ……………6分
(Ⅱ)令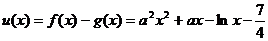 ,
,
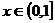
若存在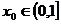 ,使
,使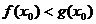 ,即
,即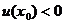 成立
成立
只需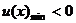 ……………7分
……………7分
由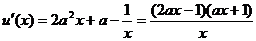 (
(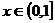 ,
,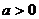 )知
)知
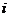 )若
)若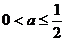 ,则
,则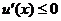 对于
对于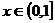 恒成立.
恒成立.
∴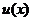 在
在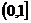 上单调递减,而
上单调递减,而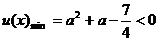 显然成立.
显然成立.
∴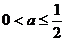 ……………9分
……………9分
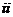 )若
)若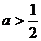 ,同理可得
,同理可得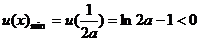
∴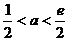 ……………11分
……………11分
综上所述, 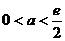 ……………12分
……………12分
 .解:(Ⅰ)设
.解:(Ⅰ)设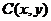 为轨迹E上任意一点,显然A、B、C不共线,∴
为轨迹E上任意一点,显然A、B、C不共线,∴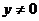 ……1分
……1分
则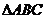 的重心
的重心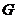 为
为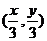 ,∵
,∵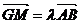 ∴
∴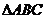 的外心
的外心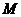 为
为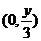 ……3分
……3分
由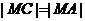
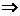
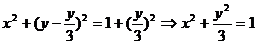
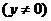 ……………6分
……………6分
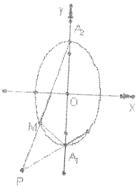 即点C的轨迹E的方程为:
即点C的轨迹E的方程为: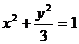
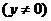
(Ⅱ)设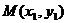 ,
,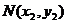 为轨迹E上
为轨迹E上
满足条件的点
∵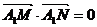
∴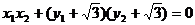 ……………8分
……………8分
而直线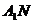 的方程为:
的方程为: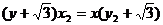 ……………(1)
……………(1)
直线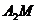 的方程为:
的方程为: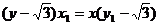 ……………(2)
……………(2)
由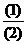 得:
得: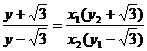
∵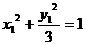 ∴
∴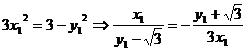
∴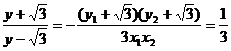 ,
,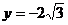
即直线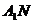 和
和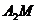 交点P恒在定直线
交点P恒在定直线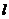 :
: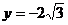 上……………12分
上……………12分
(Ⅱ)法2:设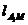 :
: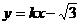 ,则
,则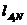 :
: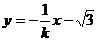
由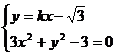
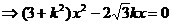
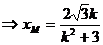 ,
,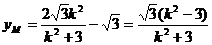
∴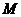 的坐标为
的坐标为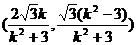 ……………9分
……………9分
∴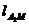 为:
为: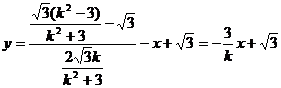 ……………10分
……………10分
联立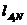 的方程,解得:
的方程,解得: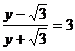 ∴
∴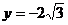
即点P恒在定直线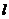 :
: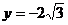 上。……………12分
上。……………12分
 .解:(Ⅰ)
.解:(Ⅰ)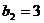 ,
,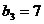 ,
,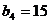 ……………1分
……………1分
由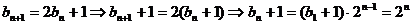
∴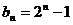 …………………………3分
…………………………3分
(Ⅱ)∵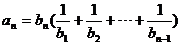
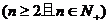
∴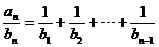 ,
,
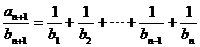
∴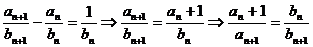
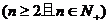 ………………6分
………………6分
(Ⅲ)由(Ⅱ)知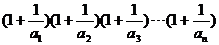
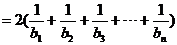 ………………9分
………………9分
而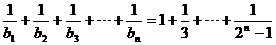 ………………10分
………………10分
当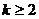 时,
时,
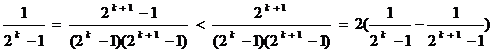
………………12分
法1:∴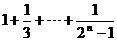
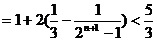 ………………13分
………………13分
∴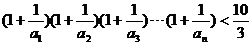 ………………14分
………………14分
法2:原不等式只需证:
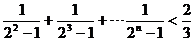 ………………11分
………………11分
∵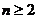 时,
时,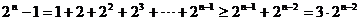
∴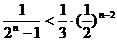 ………………13分
………………13分
∴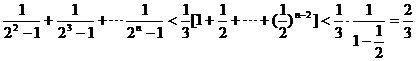
………………14分