1.已知数列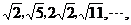 则
则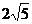 是这个数列的( )
是这个数列的( )
(A) 第六项 (B) 第七项 (C) 第八项 (D)第九项
2.等差数列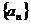 的前
的前 项和为
项和为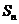 ,若
,若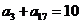 则
则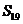 ( )
( )
(A) 55 (B)
3.在△ABC中,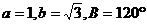 ,则A等于 ( )
,则A等于 ( )
(A)30° (B) 45° (C) 60° (D) 120°
4.在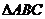 中,已知
中,已知 ,则
,则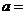 ( )
( )
(A)2; (B)1; (C)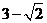 ; (D)
; (D)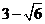 .
.
5.已知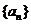 是公比为
是公比为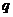 的等比数列,且
的等比数列,且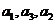 成等差数列,则
成等差数列,则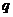 等于( )
等于( )
(A)1; (B)-2; (C)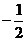 ; (D)1或
; (D)1或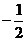 .
.
6.将9个数排成如下图所示的数表,若每行3个数按从左至右的顺序构成等差数列,每列的
3个数按从上到下的顺序也构成等差数列,且表正中间一个数a22=2,则表中所有数之和
为 ( )

(A) 20 (B) 18 (C) 512 (D) 不确定的数
7.在△ABC中,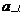
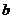
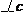 分别是∠A、∠B、∠C的对边,且
分别是∠A、∠B、∠C的对边,且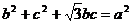 ,
,
则∠A等于( )
(A) 60° (B) 30° (C) 120° (D) 150°
8.在数列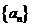 中,已知
中,已知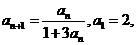 则
则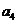 等于( )
等于( )
(A) 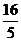 (B)
(B)
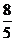 (C)
(C)
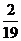 (D)
(D)
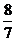
9.设 ,那么数列a、b、c是 ( )
,那么数列a、b、c是 ( )
(A) 是等差数列但不是等比数列 (B) 是等比数列但不是等差数列
(C) 既是等比数列又是等差数列 (D) 既不是等比数列又不是等差数列
11.某人朝正东方向走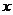 千米后,向右转
千米后,向右转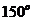 并走
并走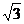 千米,
千米,
那么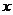 的值为 ( )
的值为 ( )
(A) 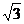 (B)
(B)
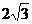 (C)
(C) 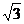 或
或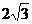 (D) 3
(D) 3
12.在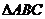 中,若
中,若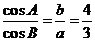 ,则
,则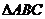 是 ( )
是 ( )
(A) 直角三角形 (B) 等腰三角形
(C) 等腰或直角三角形 (D) 钝角三角形
13.在△ABC中,若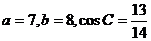 ,则最大角的余弦是(
)
,则最大角的余弦是(
)
(A) 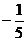 (B)
(B)
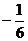 (C)
(C)
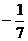 (D)
(D)
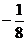
14.已知等比数列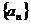 的前n项和为
的前n项和为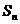 ,且
,且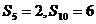 ,则
,则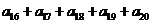
的值是 ( )
(A) 54 (B)
15.等差数列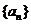 中,
中,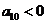 ,
,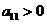 ,且
,且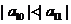 ,
,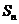 为其前
为其前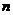 项之和,则( )
项之和,则( )
(A)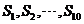 都小于零,
都小于零,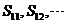 都大于零
都大于零
(B)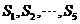 都小于零,
都小于零,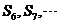 都大于零
都大于零
(C)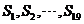 都小于零,
都小于零,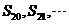 都大于零
都大于零
(D)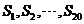 都小于零,
都小于零,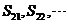 都大于零
都大于零
16.若数列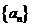 的前
的前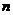 项和
项和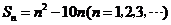 ,则此数列的通项公式为
,则此数列的通项公式为
17.在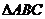 中,
中,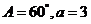 ,则
,则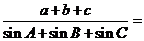
18.在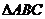 中,三个内角
中,三个内角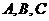 成等差数列,对应三边
成等差数列,对应三边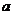 、
、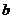 、
、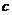 成等比数列,
成等比数列,
则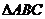 的形状是 .
的形状是 .
19.给定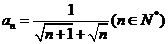 ,则使
,则使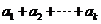 为整数的最小正整数
为整数的最小正整数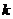 的值
的值
是
20.等差数列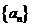 中,
中,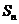 是它的前
是它的前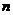 项之和,且
项之和,且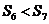 ,
,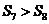 ,则
,则
①数列的公差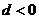 ②
②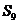 一定小于
一定小于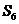
③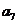 是各项中最大的一项 ④
是各项中最大的一项 ④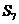 一定是
一定是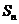 n中的最大值
n中的最大值
其中正确的是_______________________(填入你认为正确的所有序号).
21(本小题满分6分)
已知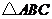 的周长为
的周长为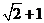 ,且
,且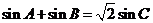 .
.
(I)求边 的长;
的长;
(II)若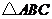 的面积为
的面积为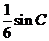 ,求角
,求角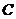 的度数.
的度数.
22.(本题满分7分)
已知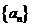 是等差数列,其中
是等差数列,其中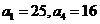
(Ⅰ)求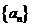 的通项;
的通项;
(Ⅱ)数列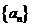 从哪一项开始小于0;
从哪一项开始小于0;
(Ⅲ)求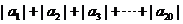 值。
值。
23(本题满分7分)
在△ABC中,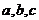 分别是
分别是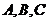 的对边,且
的对边,且

(Ⅰ)求角B的大小;
(Ⅱ)若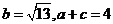 ,求
,求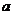 的值;
的值;
24.(本小题满分7分)
在等比数列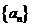 中,
中,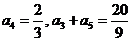 .
.
(I)求数列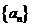 的通项公式;
的通项公式;
(II)若数列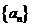 的公比大于
的公比大于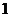 ,且
,且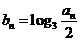 ,求数列
,求数列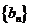 的前
的前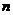 项和
项和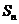 .
.
25(本题满分8分)
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n 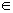 N+,都有
N+,都有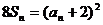 。
。
(Ⅰ)写出数列{an}的前3项;
(Ⅱ)证明数列{an}是等差数列,并求其通项公式(写出推证过程);
(Ⅲ)设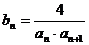 ,
,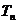 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得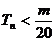 对所有n
对所有n 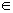 N+都成立的最小正整数
N+都成立的最小正整数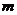 的值。
的值。
长山中学2008级第二学期第一学段

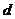 不为0,
不为0,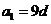

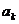 是
是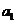 与
与 的等比中项,则
的等比中项,则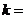 ( )
( )