1、在空间下列命题正确的是………………………………………………………………( )
(A)分别在两个平面内的直线叫做异面直线
(B)和两条异面直线都垂直的直线叫做两条异面直线的公垂线
(C)过直线外一点只有一条直线和这条直线垂直
(D)一条直线与平面平行,则它与平面内的无数条直线平行
2、下列命题中,a、b、c表示不同的直线,α、β表示不同的平面,其真命题共有( )
①若a⊥b,b⊥α,则a∥α ②若a⊥α,b⊥α,则a∥b,
③a是α的斜线,b是a在α上的射线,c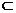 α,a⊥c,则b⊥c
α,a⊥c,则b⊥c
④若a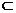 α,b
α,b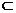 α,c⊥a,c⊥b,则c⊥α
α,c⊥a,c⊥b,则c⊥α
(A)1个 (B)2个 (C)3个 (D)4个
3、在平行四边形ABCD所在平面外有一点P,使PA=PB=PC=PD,则平行四边形一定是…………………………………………………………………………………………( )
(A)菱形 (B)矩形 (C)菱形或矩形 (D)正方形
4、在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方体形折成一个四面体,使B、C、D三点重合,重合后的点为P,那么四面体A―EFP中必有………………………………………………………………………………( )
(A)AG⊥平面EFP (B)AP⊥平面EFP (C)PF⊥平面AEF (D)PC⊥平面AEF
5、A、B、C、D是空间不共面的四点,且AB⊥CD,AD⊥BC,则直线BD与AC的关系是……………………………………………………………………………………………( )
(A)平行 (B)相交 (C)垂直 (D)异面
6、一条长为a的线段,夹在互相垂直的两个平面之间,它和这两个平面所成的角分别是45°和30°,由这线段两端向两平面的交线引垂线,则垂足间的离是………………………( )
(A) (B)
(B)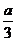 (C)
(C)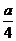 (D)
(D)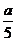
7、正方体ABCD-A1B1C1D1中,E是BC的中点,则平面B1D1E与平面ABCD所成的二面角的正弦值为……………………………………………………………………………………( )
(A)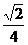 (B)
(B) (C)
(C)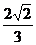 (D)1
(D)1
8、正三棱柱ABC-A1B1C1中,AB=AA1,则AC1与平面BB1C1C所成角的正弦值为( )
(A)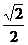 (B)
(B)
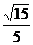 (C)
(C)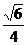 (D)
(D)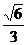
9、等边△ABC的边长为1,BC边上的高为AD,沿高AD折成直二面角,则A到BC的距离为…………………………………………………………………………………………( )
(A)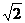 (B)
(B)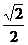 (C)
(C)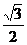 (D)
(D)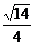
10、棱长为a的正方体ABCD-A1B1C1D1,异面直线A1B和B1C的距离为………( )
(A)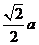 (B)
(B)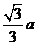 (C)
(C) (D)
(D)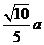
11、一个正四棱锥的一个对角面与一个侧面的面积比为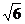 ∶2,则其侧面与底面所成的角为……………………………………………………………………………………………( )
∶2,则其侧面与底面所成的角为……………………………………………………………………………………………( )
(A)15° (B)30° (C)45° (D)60°
12、A是直径为25的球面上的一点,在这个球面上有一圆,圆上所有的点到A的距离都12,那么这个圆的半径是……………………………………………………………………( )
(A)12 (B)10 (C)15 (D)8
13、等腰△ABC和等腰Rt△ABD有公共的底边AB,它们所在的平面成60°角,若AB=16cm,AC=17cm,则CD=_______.
14、空间三条射线PA、PB、PC,∠BPC=90°,则二面角B-PA-C的余弦值为________.
15、Rt△ABC在平面α内,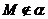 ,M到点A、B、C的距离均为b,斜边AC长为a,则点M到平面α的距离为_______.
,M到点A、B、C的距离均为b,斜边AC长为a,则点M到平面α的距离为_______.
16、长方体全面积为24cm2,各棱长总和为24cm,则其对角线长为_______.
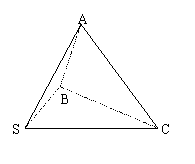 17、(12分)如图,过S点引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC
17、(12分)如图,过S点引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC
=60°,∠BSC=90°,求证:平面ABC⊥平面BSC
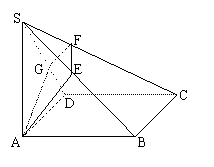 18(12分)已知:SA⊥正方形ABCD所成的平面α,SC⊥截面AEFG(如图),
18(12分)已知:SA⊥正方形ABCD所成的平面α,SC⊥截面AEFG(如图),
求证:(1)AE⊥SB,AG⊥SD (2)AF⊥GE
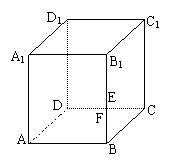 19(12分)在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点,(1)证明AD⊥D1F
19(12分)在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点,(1)证明AD⊥D1F
(2)求AE与D1F所成的角.
20(12分)如图正三棱柱ABC-A1B1C1的各棱均相等,D是BC上的一点,AD⊥C1D
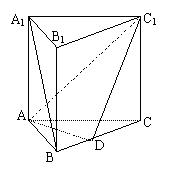 (1)求证:面ADC1⊥侧面BCC1B1
(1)求证:面ADC1⊥侧面BCC1B1
(2)求二面角C-AC1-D的大小(用反正弦表示);
(3)若AB=2,求直线A1B与截面ADC1之间的距离
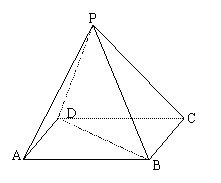 21(12分)如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2a, △PDC是正三角形,BC⊥PD
21(12分)如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2a, △PDC是正三角形,BC⊥PD
(1)求证:平面PBD⊥平面ABC; (2)求二面角C-PD-B的正切值;
(3)求点B到平面PAD的距离.。
22(14分)如图,直三棱柱ABC―A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
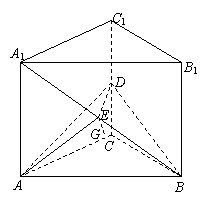 (1)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(1)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(2)求点A1到平面AED的距离.

