1、⊙C: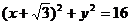 内部一点A(
内部一点A(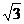 ,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程.
,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程.
2、已知A(0,7)、B(0,-7),C(12,2),以C为焦点的椭圆经过点A、B,求此椭圆的另一个焦点F的轨迹方程.
1、线段AB的两端点分别在两互相垂直的直线上滑动,且 ,求AB的中点P的轨迹方程。
,求AB的中点P的轨迹方程。
2、一条曲线在x轴上方,它上面的每一个点到点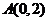 的距离减去它到x轴的距离的差都是2,求这条曲线的方程。
的距离减去它到x轴的距离的差都是2,求这条曲线的方程。
1、△ABC中,B(-3,8)、C(-1,-6),另一个顶点A在抛物线y2=4x上移动,求此三角形重心G的轨迹方程.
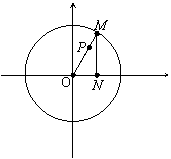
2、已知M是圆O:x2+y2=a2(a>0)上任意一点,M在x轴上的射影为N,在线段OM上取点P 使得|OP|=|MN|,求点P的轨迹方程.
〖能力测试〗 姓名 得分
1、P是椭圆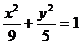 上一点,过P作其长轴垂线,M是垂足,则PM中点轨迹方程为………( )
上一点,过P作其长轴垂线,M是垂足,则PM中点轨迹方程为………( )
(A) 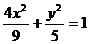 (B)
(B) 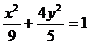 (C)
(C)  (D)
(D) 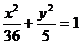
2、抛物线y2=4x关于直线x=2对称的抛物线方程为……………………………………………( )
(A) y2=-4(x-4) (B) y2=-4(x+4) (C)y2=4(x-4) (D) y2=4(x+4)
3、动点P在抛物线y=2x2+1上移动,则点P与点A(0,-1)连线中点M轨迹方程是……( )
(A) y=2x2 (B) y=6x2 (C)y=4x2 (D) y=8x2
4、方程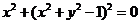 的图象是……………………………………………………………( )
的图象是……………………………………………………………( )
(A)y轴或圆 (B)两点(0,1)与(0,-1)(C)y轴或直线y=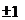 (D)以上答案均不对
(D)以上答案均不对
5、下列命题中:
①设A(2,0),B(0,2),则线段AB的方程是
②到原点的距离等于5的动点的轨迹是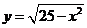
③到两坐标轴距离相等的点的轨迹方程是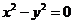
其中正确的命题有 ………………………………………………………………………………( )
(A)0个 (B)1个 (C)2个 (D)3个
6、△ABC中,三边a、b、c成等差数列,A(-1,0)、C(1,0),则顶点B的轨迹方程为
.
7、抛物线y2=x+1,定点A(3,1),B是抛物线上任意一点,点P在AB上满足BP:PA=1:2,当点B在抛物线上运动时,求点P的轨迹方程并指出轨迹是什么曲线?
圆锥曲线中的对称问题
〖考试内容〗理解中心对称和轴对称的概念,掌握求点和曲线关于直线的对称点或者对称曲线的一般方法,熟练掌握几种特殊曲线的对称问题.
〖复习要求〗掌握中心对称的实质――中点问题;轴对称的实质――中点与斜率问题;掌握点关于点、原点、x轴、y轴、直线y=±x+m、x=a、y=b的对称点.
〖知识点训练〗
1、点A(a,0)、B(4,b)关于点C(2,3)对称,则a= ;b= ;
2、曲线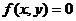 关于直线y=x+b对称曲线方程为 ;
关于直线y=x+b对称曲线方程为 ;
3、⊙C:x2+y2+4x-12y+39=0关于直线l:3x+my-12=0对称,则实数m= ;
4、设曲线xy=1与⊙C:x2+y2-4x-4y+3=0交于A、B两点,则AB的中垂线方程为 .
〖例题分析〗
1、求抛物线C:y2-2x-4y+6=0关于下列元素的对称曲线:
⑴点(0,1);
⑵直线x+y-1=0;
2、如抛物线y=x2+3x-1上存在两个不同点关于直线x+y=0对称,求出这两个点的坐标.
3、(2003年上海高考题,16分=4分+5分+7分)在以O为原点的直角坐标系中,A(4,-3)为直角三角形OAB的直角顶点,已知|AB|=2|OA|,并且点B的纵坐标大于零.
①求向量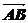 的坐标;
的坐标;
②求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
③是否存在实数a,使得抛物线y=ax2-1上的点总有关于直线OB对称的两个点?如果有,求出a的取值范围,如果不存在,说明理由!
〖课堂练习〗
1、曲线y2=|x|+1的对称轴为………………………………………………………………………( )
(A)x轴 (B)y轴 (C)x轴或y轴 (D)直线y=±x
2、椭圆 关于点A(-2,1)对称的椭圆方程为
.
关于点A(-2,1)对称的椭圆方程为
.
〖能力测试〗 姓名 得分
1、关于曲线x3-y3+9x2y+9xy2=0,有如下命题:⑴关于原点对称;⑵关于y轴对称;⑶关于x轴对称;⑷关于直线y=x对称;⑸关于直线y+x=0对称.其中正确命题个数有……………( )
(A)1 (B)2 (C)3 (D) 4
2、曲线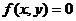 关于直线x=a对称曲线方程为……………………………………………( )
关于直线x=a对称曲线方程为……………………………………………( )
(A) 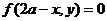 (B)
(B)  (C)
(C)  (D)
(D) 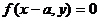
3、以直线x-y+1=0为对称轴,与曲线x2+y2-x+2y=0对称的曲线方程是…………………( )
(A) x2+y2-4x+3y+5=0 (B) x2+y2+4x+3y+5=0
(C) x2+y2-4x-3y+5=0 (D) x2+y2+4x-3y+5=0
4、“a=1”是“方程x2y+y-2ax=0的曲线关于原点对称”的……………………………………( )
(A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件 (D) 非充分非必要条件
*5、椭圆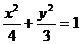 上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围.
上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围.
*6、设曲线C的方程为y=x3-x,将C沿x轴、y轴正向分别平移t、s个单位后得到曲线C1.
⑴求C1的方程;
⑵证明C、C1关于点 对称;
对称;
圆锥曲线的最值问题
〖考试内容〗掌握求函数最值的常用方法,特别是二次函数在定区间上的最值问题.
〖复习要求〗掌握求函数最值的基本程序:给出变量(可以不止一个)――求出目标函数――统一函数变量――给出变量取值范围――求最值
〖知识点训练〗
1、曲线x2+4y2-6x-24y+9=0的最高点与最低点的坐标分别是……………………………( )
(A)(3,0),(3,-6) (B)(-3,6),(-3,0) (C)(-3,0),(-3,-6) (D)(3,6),(3,0)
2、F是椭圆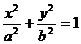 的一个焦点,直线l经过原点与此椭圆交于A、B两点,则△ABF面积最大值为…………………………………………………………………………………………( )
的一个焦点,直线l经过原点与此椭圆交于A、B两点,则△ABF面积最大值为…………………………………………………………………………………………( )
(A)ab (B)ac (C)bc (D)不能确定
3、双曲线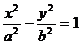 的离心率为e1、
的离心率为e1、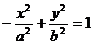 的离心率为e2,则e1+e2的最小值是( )
的离心率为e2,则e1+e2的最小值是( )
(A)4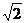 (B)2
(C)2
(B)2
(C)2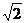 (D)4
(D)4
4、点P(x,y)在椭圆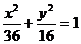 上,F是椭圆的右焦点,则|FP|max= ;|FP|min= .
上,F是椭圆的右焦点,则|FP|max= ;|FP|min= .
〖例题分析〗
1、点P(x,y)在椭圆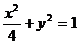 上,
上,
⑴求2x+3y的最大值;
⑵求(x-1)2+y2最小值.
2、在直线l:x-y+9=0上任意取一点P,经过P点以椭圆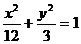 的焦点为焦点作椭圆E.
的焦点为焦点作椭圆E.
⑴P在何处时,E的长轴最短?
⑵求E长轴最短时的方程.
3、设点A(a,0),求抛物线y2=2x上的点P到A距离的最小值.
4、抛物线C的焦点在原点,顶点在x的负半轴上,直线l:x+y+m=0(m>0)与C交于A、B两点,△AOB面积最大值为2 ,求C的方程并且求当△AOB面积最大时的l方程.
,求C的方程并且求当△AOB面积最大时的l方程.
〖能力测试〗 姓名 得分
1、已知点A(3,0)、B(0,4),动点P(x,y)在线段AB上,则xy最大值为……………………( )
(A) 3
(B)
4
(C)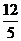 (D)
(D) 
2、定线段AB长度为4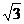 ,动点P满足|PA|+|PB|=8,O为AB中点,则|PO|最小值为……( )
,动点P满足|PA|+|PB|=8,O为AB中点,则|PO|最小值为……( )
(A) 8
(B) 4
(C)2 (D) 4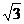
3、如果点(x,y)在椭圆4(x-2)2+y2=4上运动,则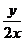 的最大值为…………………………( )
的最大值为…………………………( )
(A)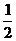 (B) -
(B) -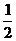 (C)-
(C)-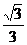 (D)
(D)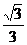
4、椭圆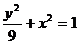 的内接矩形面积最大值为
.
的内接矩形面积最大值为
.
5、P点是椭圆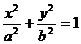 上一点,F1、F2是焦点,则|PF1|・|PF2|最大时,P的坐标为
.
上一点,F1、F2是焦点,则|PF1|・|PF2|最大时,P的坐标为
.
6、在抛物线y2=2x上求一点P,使得P到直线x-y+3=0的距离最小.
高三数学总复习单元测试――圆锥曲线
姓名 得分 .
1、抛物线y2=ax (a≠0)的准线方程是………………………………………………………… ( )
(A)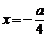 (B)
(B)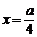 (C)
(C)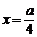 或
或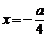 (D)
(D)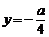
2、若椭圆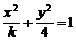 的一条准线的方程是x=5,则k 的值是………………………………( )
的一条准线的方程是x=5,则k 的值是………………………………( )
(A)5
(B)5或20 (C)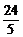 (D)
(D)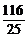
3、双曲线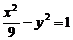 的两个焦点F1,F2,A是此双曲线上一点,且|AF1|=5,那么|AF2|=……( )
的两个焦点F1,F2,A是此双曲线上一点,且|AF1|=5,那么|AF2|=……( )
(A)11 (B)8 (C)11或1 (D)8或2
4、椭圆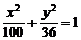 上的点P到它的左准线的距离是10,则P点到它的右焦点的距离为……( )
上的点P到它的左准线的距离是10,则P点到它的右焦点的距离为……( )
(A)8 (B)28 (C)2 (D)12
5、对l≠0的任何实数值,双曲线 与
与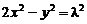 都有相同的:①焦点;②准线;③渐近线;④离心率. 以上四个结论中,正确的………………………………………………( )
都有相同的:①焦点;②准线;③渐近线;④离心率. 以上四个结论中,正确的………………………………………………( )
(A)①② (B)③④ (C)①③ (D)②④
6、P是抛物线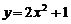 上的动点,A(0,-1),则线段PA的中点的轨迹方程是…………( )
上的动点,A(0,-1),则线段PA的中点的轨迹方程是…………( )
(A)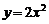 (B)
(B)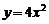 (C)
(C) (D)
(D)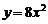
7、过抛物线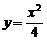 的焦点作直线交抛物线于两点
的焦点作直线交抛物线于两点 ,如果
,如果 ,那么线段AB的长为……………………………………………………………………………………( )
,那么线段AB的长为……………………………………………………………………………………( )
(A)12 (B)10 (C)8 (D)6
8、双曲线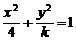 的离心率
的离心率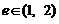 ,则k的取值范围是………………………………(
)
,则k的取值范围是………………………………(
)
(A)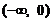 (B)
(B)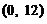 (C)
(C)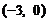 (D)
(D)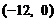
9、F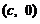 为椭圆
为椭圆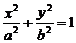 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F的距离等于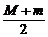 的点的坐标是…………………………………………………( )
的点的坐标是…………………………………………………( )
(A) (B)
(B)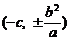 (C)
(C)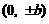 (D)
(D)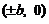
10、若抛物线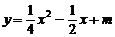 的焦点在x轴上,则m的值是………………………………( )
的焦点在x轴上,则m的值是………………………………( )
(A)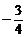 (B)
(B) (C)
(C)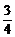 (D)
(D)
11、椭圆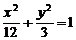 的焦点是F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的………………………………………………………………………………………( )
的焦点是F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的………………………………………………………………………………………( )
(A)7倍 (B)5倍 (C)4倍 (D)3倍
12、以双曲线 的中心O为顶点,以其左准线为准线的抛物线与此双曲线的右准线交于A、B,则△AOB的面积等于…………………………………………………………………( )
的中心O为顶点,以其左准线为准线的抛物线与此双曲线的右准线交于A、B,则△AOB的面积等于…………………………………………………………………( )
(A)81
(B)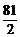 (C)
(C)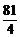 (D)
(D)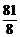
13、已知椭圆的焦点F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|与|PF2|的等差中
项,则该椭圆的方程是 .
14、平移双曲线x2-3y2+2x-2=0,把它的中心移到右焦点处,此时双曲线的渐近线方程是 .
15、已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p= .
16、对于椭圆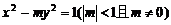 ,给出下列命题:①焦点在x轴上;②短半轴的长为1;③准线方程是
,给出下列命题:①焦点在x轴上;②短半轴的长为1;③准线方程是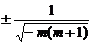 ;④离心率
;④离心率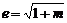 . 其中正确命题的序号是
.
. 其中正确命题的序号是
.
17、(本小题满分12分)已知椭圆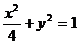 的焦点为F1、F2,抛物线
的焦点为F1、F2,抛物线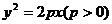 与此椭圆在第一象限交点为Q,如果
与此椭圆在第一象限交点为Q,如果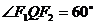 ,求:
,求:
⑴△F1QF2的面积;⑵抛物线方程。
18、(本小题满分12分)顶点在原点,焦点在x轴上的抛物线截直线2x-y-4=0所得的弦长为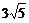 ,求此抛物线的方程.
,求此抛物线的方程.
19、(本小题满分12分)抛物线的顶点在原点,焦点是椭圆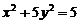 的左焦点,过点M(-1,1)引抛物线的弦使点M为弦的中点,求弦所在的直线方程,并求出弦长.
的左焦点,过点M(-1,1)引抛物线的弦使点M为弦的中点,求弦所在的直线方程,并求出弦长.
20、(本小题满分12分)已知双曲线两顶点的坐标为(2,-1)和(2,5),并且它的一条渐近线与直线4x-3y=0平行,求此双曲线的方程,并求它的焦点坐标和两条条渐近线的方程.
21、(本小题满分12分)已知动圆C与定圆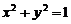 内切,与直线l:x=3相切.
内切,与直线l:x=3相切.
(Ⅰ)求动圆圆心C的轨迹方程;
(Ⅱ)若Q是上述轨迹上的点,求Q到点距离的最小值.
22、(本小题满分14分)
椭圆的中心在原点,一个顶点为A(0,-1),焦点在x轴上,且右焦点到直线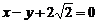
的距离为3,若纵截距为m的直线l与该椭圆交于不同两点M、N,当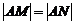 时,试求m
时,试求m
及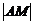 的取值范围.
的取值范围.

