1.集合 ▲ .
▲ .
2.“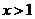 ”是“
”是“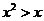 ”的 ▲ 条件.
”的 ▲ 条件.
3.在△ABC中,若(a+b+c)(b+c-a)=3bc,则A等于_____▲_______.
 4. 一个总体中的80个个体编号为0,l,2,……,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本.即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码中最大的号码是___▲ .
4. 一个总体中的80个个体编号为0,l,2,……,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本.即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码中最大的号码是___▲ .
5.已知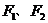 为椭圆
为椭圆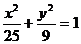 的两个焦点, 过
的两个焦点, 过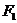 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若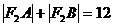 ,则
,则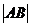 =_____▲____.
=_____▲____.
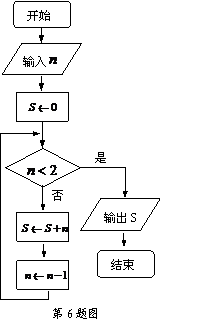
则输出的变量 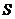 的值是 ▲ .
的值是 ▲ .
7.已知t为常数,函数 在区间[0,3]上的最大值为2,则t=▲
在区间[0,3]上的最大值为2,则t=▲
8.已知点P在抛物线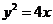 上,那么点P到点
上,那么点P到点 的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为__▲ .
的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为__▲ .
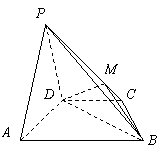
 9.如图,已知球O点面上四点A、B、C、D,
9.如图,已知球O点面上四点A、B、C、D,
DA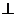 平面ABC,AB
平面ABC,AB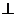 BC,DA=AB=BC=
BC,DA=AB=BC=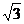 ,
,
则球O点体积等于_____▲______.
10.定义:区间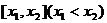 的长度为
的长度为 .
.
已知函数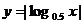 定义域为
定义域为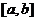 ,值域为
,值域为
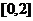 ,则区间
,则区间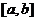 的长度的最大值为▲ .
的长度的最大值为▲ .
11、椭圆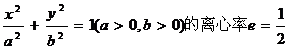 ,右焦点F(c,0),
,右焦点F(c,0),
方程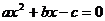 的两个根分别为x1,x2,则点P(x1,x2)在与圆
的两个根分别为x1,x2,则点P(x1,x2)在与圆
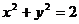 的位置关系是___▲ .
的位置关系是___▲ .
12. 设{an}是正项数列,其前n项和Sn满足:4Sn=(an-1)(an+3),则数列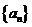 的通项公式
的通项公式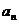 = ▲ .
= ▲ .
13.若从点O所作的两条射线OM、ON上分别有点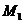 、
、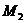 与点
与点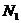 、
、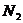 ,则三角形面积之比为:
,则三角形面积之比为: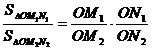 . 若从点O所作的不在同一个平面内的三条射线OP、OQ和OR上分别有点
. 若从点O所作的不在同一个平面内的三条射线OP、OQ和OR上分别有点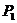 、
、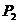 与点
与点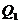 、
、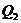 和
和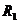 、
、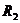 ,则类似的结论为:__ ▲
,则类似的结论为:__ ▲
14. 方程 在区间
在区间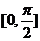 上有两个不同的解,则实数m的取值范围是______▲_____
上有两个不同的解,则实数m的取值范围是______▲_____
15、(本题满分14分)
不等式组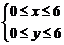 表示的区域为A,不等式组
表示的区域为A,不等式组 表示的区域为B,在区域A中任意取一点P
表示的区域为B,在区域A中任意取一点P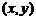 .
.
(Ⅰ)求点P落在区域B中的概率;
(Ⅱ)若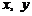 分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
16.(本题满分14分)
矩形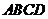 的两条对角线相交于点
的两条对角线相交于点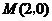 ,
,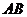 边所在直线的方程为
边所在直线的方程为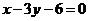 ,点
,点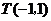 在
在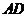 边所在直线上.
边所在直线上.
(1)求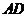 边所在直线的方程;(7分)
边所在直线的方程;(7分)
(2)求矩形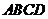 外接圆的方程。(7分)
外接圆的方程。(7分)
17、(本题满分15分)
如图,在四棱锥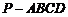 中,平面
中,平面 平面
平面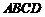 ,
, ,
,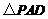 是等边三角形,已知
是等边三角形,已知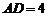 ,
,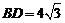 ,
,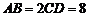 .
.
(Ⅰ)设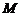 是
是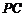 上的一点,证明:平面
上的一点,证明:平面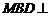 平面
平面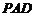 ;
;
(Ⅱ)当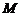 点位于线段PC什么位置时,
点位于线段PC什么位置时, 平面
平面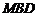 ?
?
(Ⅲ)求四棱锥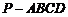 的体积.
的体积.
18、(本题满分15分)
已知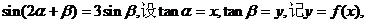
(1)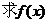 的解析表达式;
的解析表达式;
(2)若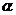 角是一个三角形的最小内角,试求函数
角是一个三角形的最小内角,试求函数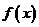 的值域.
的值域.
19、(本小题16分)
假设A型进口车关税税率在2003年是100%,在2008年是25%,在2003年A型进口车每辆价格为64万元(其中含32万元关税税款)
(1)已知与A型车性能相近的B型国产车,2003年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2008年B型车的价格不高于A型车价格的90%,B型车价格要逐年等额降低,问每年至少下降多少万元?
(2)某人在2003年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带利息是否一定够买按(1)中所述降价后的B型车一辆?(参考数据:1.0185≈1.093)
20、(本题满分16分)
已知二次函数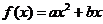 +
+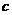 的图象通过原点,对称轴为
的图象通过原点,对称轴为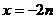 ,
,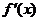 是
是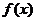 的导函数,且
的导函数,且
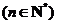 .
.
(I)求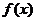 的表达式;
的表达式;
(II)若数列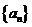 满足
满足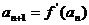 ,且
,且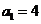 ,求数列
,求数列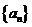 的通项公式;
的通项公式;
(III)若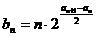 ,
,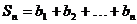 ,是否存在自然数M,使得当
,是否存在自然数M,使得当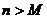 时
时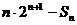
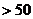 恒成立?若存在,求出最小的M;若不存在,说明理由.
恒成立?若存在,求出最小的M;若不存在,说明理由.
泰兴市第三高级中学高三数学(文)考前指导一