1.计算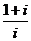 的结果是( )
的结果是( )
A.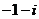 B.
B.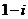 C.
C.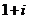 D.
D.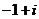
2.抛物线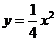 在点
在点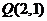 处的切线方程是( )
处的切线方程是( )
A.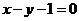 B.
B.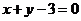 C.
C.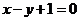 D.
D.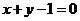
3.在复平面内,复数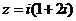 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.设函数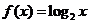 ,则
,则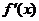 等于( )
等于( )
A.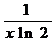 B.
B.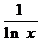 C.
C.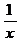 D.
D.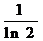
5. 计算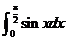 的结果是( )
的结果是( )
A.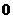 B.
B.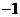 C.
C.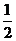 D.
D.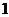
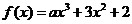 ,若
,若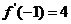 ,则
,则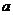 的值等于( )
的值等于( )
A.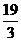 B.
B.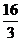 C.
C.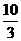 D.
D.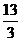
6B.函数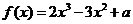 的极大值为
的极大值为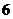 ,那么
,那么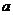 的值是( )
的值是( )
A.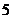 B.
B. 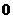 C.
C.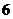 D.
D.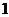
7. 一质点做直线运动,由始点经过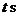 后的距离为
后的距离为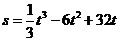 ,则速度为
,则速度为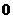 的时刻是( )
的时刻是( )
A.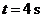 B.
B.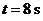 C.
C.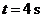 与
与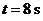 D.
D.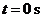 与
与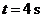
8. 有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线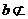 平面
平面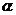 ,直线
,直线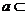 平面
平面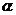 ,直线
,直线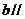 平面
平面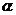 ,则直线
,则直线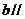 直线
直线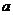 ” .结论显然是错误的,这是因为( )
” .结论显然是错误的,这是因为( )
A.大前提错误 B.推理形式错误 C.小前提错误 D.非以上错误
9. 右图是函数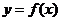 的导函数
的导函数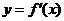 的图象,
的图象,
 给出下列命题:
给出下列命题:
①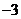 是函数
是函数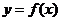 的极值点;
的极值点;
②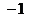 是函数
是函数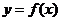 的最小值点;
的最小值点;
③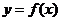 在
在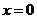 处切线的斜率小于零;
处切线的斜率小于零;
④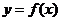 在区间
在区间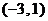 上单调递增.
上单调递增.
则正确命题的序号是( )
A.①② B.①④ C.②③ D.③④
10. 由直线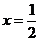 ,
,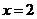 ,曲线
,曲线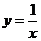 及
及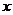 轴所围成的图形的面积是( )
轴所围成的图形的面积是( )
A. 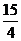 B.
B. 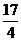 C.
C. 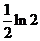 D.
D. 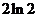
11.设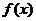 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且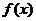 满足:“当
满足:“当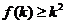 成立时,总可以推出
成立时,总可以推出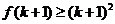 成立”.那么,下列命题总成立的是( )
成立”.那么,下列命题总成立的是( )
A.若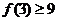 成立,则当
成立,则当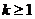 时,均有
时,均有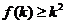 成立
成立
B.若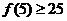 成立,则当
成立,则当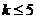 时,均有
时,均有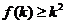 成立
成立
C.若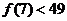 成立,则当
成立,则当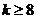 时,均有
时,均有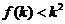 成立
成立
D.若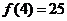 成立,则当
成立,则当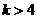 时,均有
时,均有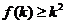 成立
成立
12.已知数列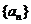 满足
满足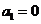 ,
,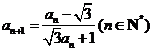 ,则
,则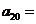 ( )
( )
A.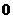 B.
B. C.
C.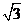 D.
D.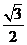
13. 若复数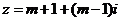 为纯虚数,则实数
为纯虚数,则实数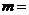 ____________.
____________.
14. 用演绎法证明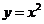 在区间
在区间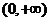 为增函数时的大前提是____________.
为增函数时的大前提是____________.
15. 在平面,到一条直线的距离等于定长(为正数)的点的集合是与该直线平行的两条直线.这一结论推广到空间则为:在空间,到一个平面的距离等于定长的点的集合是 .
16.曲线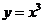 在点
在点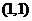 处的切线与
处的切线与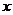 轴、直线
轴、直线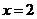 所围成的三角形的面积为__________.
所围成的三角形的面积为__________.
17. (本小题满分12分)
已知二次函数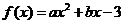 在
在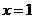 处取得极值,且在
处取得极值,且在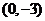 点处的切线与直线
点处的切线与直线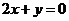 平行.
平行.
(Ⅰ)求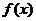 的解析式;
的解析式;
(Ⅱ)求函数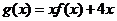 的单调递增区间.
的单调递增区间.
设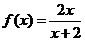 ,
,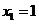 ,
,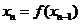
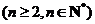 .
.
(Ⅰ)求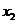 ,
,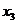 ,
,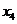 的值;
的值;
(Ⅱ)归纳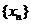 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
18B. (本小题满分12分)
在数列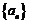 中,
中,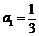 ,且
,且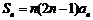 ,
,
(Ⅰ)求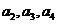 的值;
的值;
(Ⅱ)归纳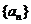 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
已知函数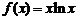 .
.
(Ⅰ)求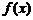 的最小值;
的最小值;
(Ⅱ)若对所有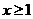 都有
都有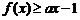 ,求实数
,求实数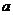 的取值范围.
的取值范围.
19 B. (本小题满分12分)
已知函数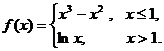
(Ⅰ)求函数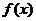 的单调减区间;
的单调减区间;
(Ⅱ)若不等式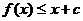 对一切
对一切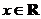 恒成立,求
恒成立,求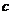 的取值范围.
的取值范围.
北京市东城区2008――2009学年度
高二年级数学选修课程模块2-2测试题(理科卷)

