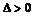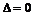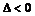29、公式法: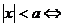 ;
;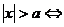 。
。
五、 一元二次不等式解法
20、二次不等式与二次函数、二次方程的关系:(其中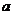 >0)
>0)
判别式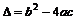
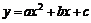
的图象
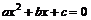
的根
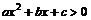
的解集
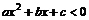
的解集
六、 逻辑联结词
21、命题:可以 的语句叫命题。
22、逻辑联结词: 叫做逻辑联结词。
23、简单命题: 的命题叫做简单命题。
24、复合命题:由 构成的命题叫做复合命题。
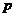 且
且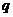
真
真
真
假
假
真
假
假
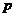 或
或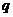
真
真
真
假
假
真
假
假
25、真值表:
非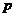
真
假
26、命题的否定:“非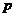 ”叫做命题
”叫做命题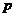 的否定。常用的正面叙述的词语及它的否定列举如下:
的否定。常用的正面叙述的词语及它的否定列举如下:
正面词语
等于
大于(>)
小于(<)
是
都是
否定
正面词语
至多有一个
至少有一个
否定
七、 四种命题:
27、原命题与 命题等价;否命题与 命题等价
原命题
若p则q
逆命题
否命题
逆否命题
28、四种命题
29、反证法:
步骤:(1)反设:假设结论不成立
(2)矛盾:从这个假设出发推出矛盾;
(3)结论:矛盾说明假设错误,因而结论正确
应用:(1)原则:正难则反
(2)适用情况:结论是否定的、结论含“至少有一个是”、证明逆定理等。
八、 充要条件:
30、如果“若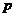 则
则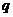 ”为真,记作 ;
”为真,记作 ;
如果“若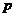 则
则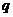 ”为假,记作 。
”为假,记作 。
31、如果已知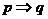 ,则
,则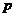 是
是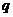 的 ;
的 ;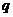 是
是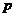 的 。
的 。
32、如果既有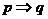 ,又有
,又有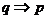 ,记作 ;则
,记作 ;则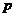 是
是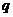 的 ;
的 ;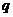 是
是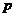 的 。
的 。
33、设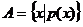 ,
,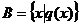 ;
;
若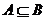 ,则
,则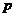 是
是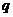 的 ;
的 ;
若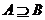 ,则
,则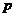 是
是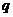 的 ;
的 ;
若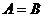 ,则
,则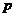 是
是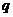 的 。
的 。