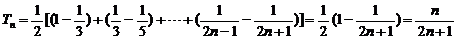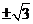13.若数列{an}为等比数列,则下面四个命题:①数列{an3}也是等比数列;②数列{-an}也是等比数列;③数列{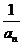 }也是等比数列;④数列{
}也是等比数列;④数列{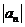 }也是等比数列,其中正确的命题是_____________________
}也是等比数列,其中正确的命题是_____________________
14.若数列{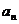 }满足
}满足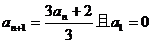 ,则
,则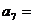 _______________________
_______________________
15.设a=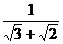 ,b=
,b=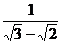 ,则a、b的等差中项为________________________
,则a、b的等差中项为________________________
16.在等比数列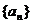 中,若
中,若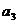 ,
,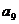 是一元二次方程
是一元二次方程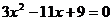 的两根,则
的两根,则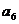 =_____________
=_____________
17.(12分)在等比数列{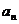 }中,已知
}中,已知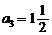 ,
,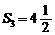 ,求
,求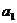 与q.
与q.
18.(12分)求数列 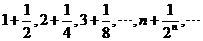 的前n项和
的前n项和
 19.(12分)在各项均为正数的等比数列{an}中, 若a5a6=9,
19.(12分)在各项均为正数的等比数列{an}中, 若a5a6=9,
求log3a1+log3a2+…+log3a10的值
20.(12分)三个数成等比数列,若第二个数加4 就成等差数列,再把第三个数加32又成等比数列,求这三个数.
21.(12分)用分期付款方式购买P4型家用电脑,价格为每台11500元,可用以下方式付款,购买当于先付1500元,以后每月交付500元,并先加付欠款利息,月利率为1%(即欠款的1%,利息不计入欠款),在交付1500元后的第一个月为分期付款的第一个月,问分期付款的第10个月交付多少钱?全部贷款付清后,买这台电脑实际花了多少钱?
22.(14分)设各项均为正数的数列{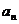 }的前n项和为Sn,且满足:
}的前n项和为Sn,且满足: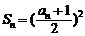 .
.
(1)求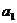 ,
,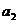 ,
,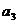 ;
;
(2)求出数列{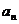 }的通项公式(写出推导过程);
}的通项公式(写出推导过程);
(3)设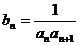 ,求数列{
,求数列{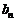 }的前n项和
}的前n项和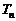 .
.
第三章 数列测试卷答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
B
A
C
C
A
D
A
B
B
A
13
①②③④
14
4
15
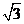
16
17.(12分)解:当q=1时,a1=a3=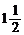 ,这时S3=3a1=
,这时S3=3a1=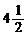 ,满足条件.
,满足条件.
当q≠1时,由已知得: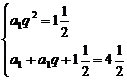 解得:
解得: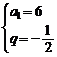
∴所求为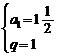 或
或 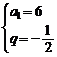 .
.
18.(12分)解: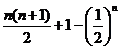
19.(12分)解:10
20.(12分)解:设这三个数为:a,aq,aq2,则
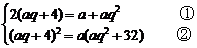
由②得: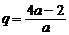 ③,代入①并整理得:9a2-20a+4=0
③,代入①并整理得:9a2-20a+4=0
解得a=2或a=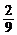
当a=2时,由③得q=3,当a=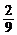 时,由③得q=-5
时,由③得q=-5
∴所求的三个数为:2,6,18 或 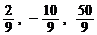 .
.
21.(12分)解:每月付500元,所欠10000元需20个月付清
第一个月付:a1=500+10000×1%=500+100=600?5(1?1)
第二个月付:a2=500+(10000-500)×1%=595=500+100?5=600?5(2?1)
第三个月付:an=500+[10000?500(n?1)]×1%=600?5(n?1)=605?5n(1≤n≤20)
当n=10时,a10=600?5(10?1)=555
∵an?an―1=(605?5n)?[605?5(n?1)=?5=d
∴S20=600×20+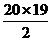 (-5)=11500
11050+1500=12550
(-5)=11500
11050+1500=12550
因此第10个月应付555元,买这电脑实际花了12550元。
22.(14分)解:(1) 由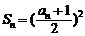 得:
得: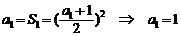
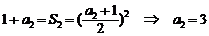 ,
,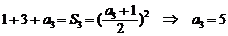
(2) 当n≥2时,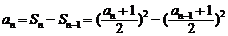
整理得:(an-1)2=(an-1+1)2 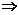 an-an-1=2
an-an-1=2
∴{an}是公差为2的等差数列,∴an=a1+(n-1)×2,an=2n-1.
(3) 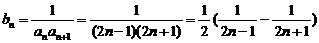
∴