1. 命题“若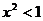 ,则
,则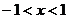 ”的逆否命题是
”的逆否命题是
(A)若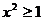 ,则
,则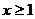 或
或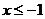 (B)若
(B)若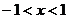 ,则
,则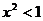
(C)若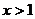 或
或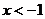 ,则
,则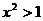 (D)若
(D)若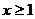 或
或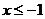 ,则
,则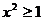
2. 集合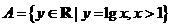 ,
,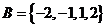 则下列结论正确的是
则下列结论正确的是
(A)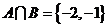 (B)
(B)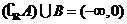
(C)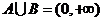 (D)
(D)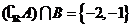
3. 已知命题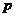 :
: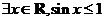 ,则
,则
(A)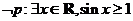 (B)
(B) 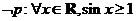
(C)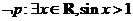 (D)
(D) 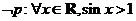
4. 已知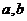 为非零实数,且
为非零实数,且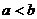 ,则下列命题成立的是
,则下列命题成立的是
(A)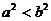 (B)
(B)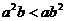 (C)
(C)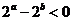 (D)
(D)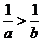
5. 若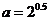 ,
, ,
,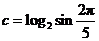 ,则
,则
(A)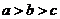 (B)
(B)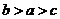 (C)
(C)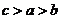 (D)
(D)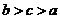
6. 若函数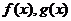 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足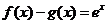 ,则有
,则有
(A)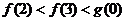 (B)
(B)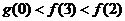
(C)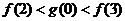 (D)
(D)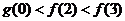
7. 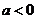 是函数
是函数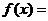
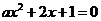 至少有一个负零点的
至少有一个负零点的
(A)必要不充分条件 (B)充分不必要条件
(C)充分必要条件 (D)既不充分也不必要条件
8. 函数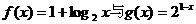 在同一直角坐标系下的图象大致是
在同一直角坐标系下的图象大致是
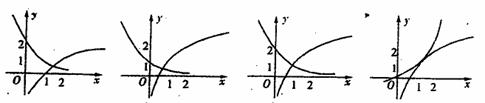 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
9. 下列结论正确的是( )
(A)当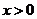 且
且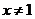 时,
时,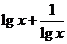
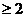 (B)
(B)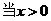 时,
时,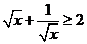
(C)当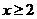 时,
时,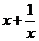 的最小值为2 (D)
的最小值为2 (D)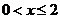 时,
时,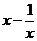 无最大值
无最大值
10.设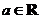 ,若函数
,若函数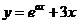 ,
,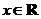 有大于零的极值点,则
有大于零的极值点,则
(A)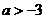 (B)
(B)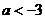 (C)
(C)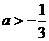 (D)
(D)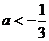
11. 设奇函数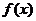 在
在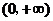 上为增函数,且
上为增函数,且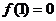 ,则不等式
,则不等式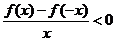 的解集为
的解集为
(A) 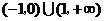 (B)
(B)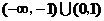
(C)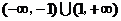 (D)
(D)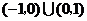
12. 设a、b、c都是正数,则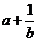 ,
,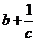 ,
,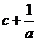 三个数
三个数
(A)都大于2 (B)至少有一个大于2
(C)至少有一个不大于2 (D)至少有一个不小于2
第Ⅱ卷 (非选择题 共90分)
注意事项:
1.第Ⅱ卷包括填空题和解答题共两个大题.
2.第Ⅱ卷所有题目的答案考生需用黑色签字笔答在 “数学”答题卡指定的位置.
13.设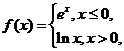 则
则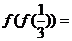 .
.
14.设曲线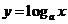 在点
在点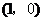 处的切线与直线
处的切线与直线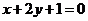 垂直,
垂直,
则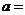 .
.
15.设定义在 上的函数
上的函数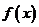 满足
满足 ,若
,若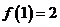 ,
,
则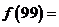 ___________________.
___________________.
16.已知定义在区间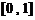 上的函数
上的函数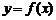 的图像如图所示,对于满足
的图像如图所示,对于满足
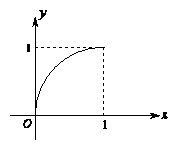
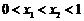 的任意
的任意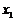 、
、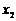 ,给出下列结论:
,给出下列结论:
①
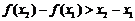 ;
;
②
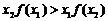 ;
;
③
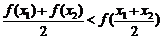 .
.
其中正确结论的序号是 .(把所有正确结论的序号都填上)
17.(本小题满分12分)
已知二次函数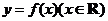 的图象过点(0,-3),且
的图象过点(0,-3),且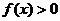 的解集
的解集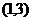 .
.
(Ⅰ)求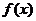 的解析式;
的解析式;
(Ⅱ)求函数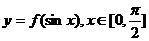 的最值.
的最值.
18.(本小题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是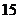 元,销售价是
元,销售价是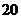 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为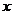
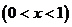 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为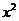 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是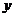 (元).
(元).
(Ⅰ)写出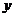 与
与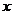 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
19.(本小题满分12分)
已知向量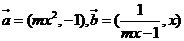 (m是常数),
(m是常数),
(Ⅰ)若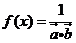 是奇函数,求m的值;
是奇函数,求m的值;
(Ⅱ)若向量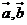 的夹角
的夹角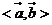 为
为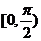 中的值,求实数
中的值,求实数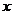 的取值范围.
的取值范围.
20.(本小题满分12分)
某公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为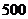 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
21.(本小题满分12分)
设p:实数x满足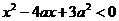 ,其中
,其中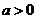 ,命题
,命题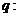 实数
实数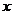 满足
满足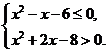 .
.
(Ⅰ)若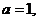 且
且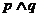 为真,求实数
为真,求实数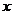 的取值范围;
的取值范围;
(Ⅱ)若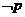 是
是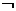
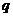 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
22.(本小题满分14分)
设函数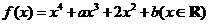 ,其中
,其中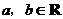 .
.
(Ⅰ)当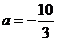 时,讨论函数
时,讨论函数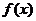 的单调性;
的单调性;
(Ⅱ)若函数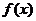 仅在
仅在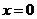 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(Ⅲ)若对于任意的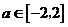 ,不等式
,不等式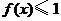 在
在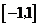 上恒成立,求
上恒成立,求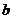 的取值范围.
的取值范围.

