析:抛物线的定义中,定点一定不在定直线上,而本题中的定点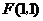 在定直线
在定直线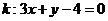 上.
上.
正:设动点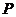 的坐标为
的坐标为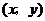 ,
,
则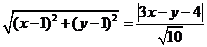 .
.
整理,得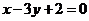 .
.
所以动点P的轨迹为直线,故选(D).
若抛物线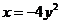 上一点
上一点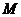 到焦点
到焦点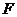 的距离为1,则点
的距离为1,则点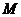 的横坐标为(
)
的横坐标为(
)
A.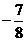 B.
B.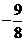 C.
C.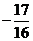 D.
D.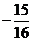
例2 抛物线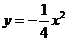 的焦点坐标是( ).
的焦点坐标是( ).
(A)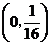 (B)
(B)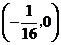
(C)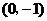 (D)
(D)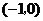
误:∵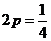 ,∴
,∴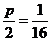 .
.
∴抛物线的焦点坐标为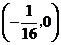 ,故选(B).
,故选(B).
析:错解是对抛物线标准方程认识不清,事实上应先化为标准方程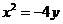 ,则
,则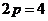 ,而不是
,而不是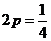 .
.
正:依题意可知,抛物线的标准方程是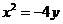 ,则
,则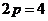 ,故
,故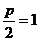 .
.
又焦点在y轴负半轴上,故其焦点坐标为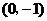 ,而选(C).
,而选(C).
例3 求以原点为顶点,坐标轴为对称轴,并且经过点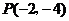 的抛物线的标准方程.
的抛物线的标准方程.
误:设抛物线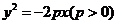 ,
,
将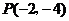 代入得
代入得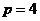 .
.
故抛物线的标准方程为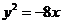 .
.
正:还有一种情形设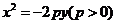 ,
,
求得标准方程为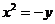 .
.
所以满足条件的抛物线的标准方程为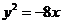 或
或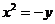 .
.
例4 动点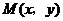 到y轴的距离比它到定点(2,0)的距离小2,求动点
到y轴的距离比它到定点(2,0)的距离小2,求动点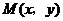 的轨迹方程.
的轨迹方程.
误:∵动点M到y轴的距离比它到定点(2,0)的距离小2,
∴动点M到定点(2,0)的距离与到定直线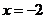 的距离相等.
的距离相等.
∴动点M的轨迹是以(2,0)为焦点,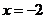 为准线的抛物线,且
为准线的抛物线,且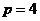 .
.
∴抛物线的方程为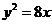 ,此即为所求动点M的轨迹方程.
,此即为所求动点M的轨迹方程.
析:错解只考虑了一种情况.在此题中,定点(2,0)到y轴的距离为2,
∴ x轴上原点左侧的点也满足题中条件.
正:由错解得M点的轨迹方程为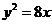 .
.
又因为x轴上(0,0)点左侧的点到y轴的距离比它到(2,0)点的距离小2,
∴ M点的轨迹方程为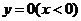 .
.
综上,得动点M的轨迹方程为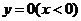 ,或
,或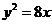 .
.

