1.已知函数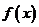 =
=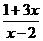 (x≠2),则其反函数
(x≠2),则其反函数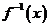 的一个单调递减区间是
的一个单调递减区间是
A.(-∞,十∞) B.(-3,+∞)
C.(3,+∞) D.以上都不对
2.已知p:不等式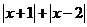 >
>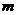 的解集为R;q:
的解集为R;q: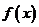 =
=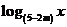 为减函数,则p成立是q成立的
为减函数,则p成立是q成立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.对于任意直线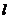 与平面
与平面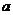 ,在平面
,在平面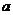 内必有直线
内必有直线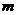 与
与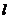
A.平行 B.相交 C.垂直 D.互为异面直线
4.已知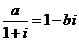 ,其中
,其中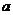 、b是实数.
、b是实数.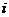 是虚数单位,则
是虚数单位,则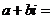
A.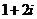 B.
B.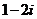 C.
C.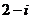 D.2
D.2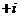
5.设全集U=R,集合M=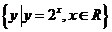 ,N=
,N=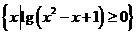 ,则下列关系式中正确的是
,则下列关系式中正确的是
A.M∩N∈M B.M∪N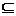 M
M
C.M∪N=R D.(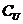 M)∩N=
M)∩N=
6.已知函数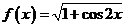 =,则
=,则
A.函数图像关于直线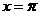 对称 B.函数图像关于点(
对称 B.函数图像关于点(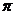 ,0)对称
,0)对称
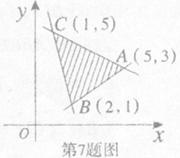 C.函数在区间
C.函数在区间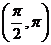 上递减 D.函数在区间
上递减 D.函数在区间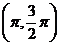 上递增
上递增
7.给出平面区域(图中阴影部分)作为可行域.其中A(5,3),B(2,1),C(1,5)。若目标函数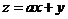 (
(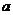 >0)取得最大值的最优解有无穷多个.则
>0)取得最大值的最优解有无穷多个.则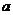 的值为
的值为
A.4 B.2
C.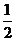 D.
D.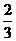
8.已知三棱锥S―ABC的四个顶点在以O为球心的同一球面上,且SA=SB=SC=AB,∠ACB=90。,则当球的表面积为400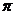 时。点O到平面ABC的距离为
时。点O到平面ABC的距离为
A.4 B.
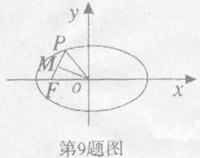 9.设P是椭圆
9.设P是椭圆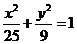 上的一点,F是椭圆的左焦点,且
上的一点,F是椭圆的左焦点,且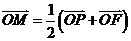 ,
,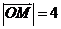 ,则点P到该椭圆左准线的距离为
,则点P到该椭圆左准线的距离为
A.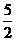 B.3
B.3
C.4 D.6
10.若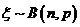 ,且
,且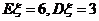 ,则P(
,则P(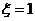 |)的值为
|)的值为
A.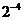 B.
B.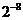 C.
C.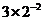 D.
D.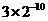
l1.若函数y=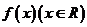 满足
满足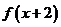 =
=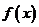 ,且
,且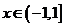 时,
时,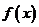 =
=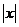 ,则函数
,则函数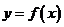 的图像与函数
的图像与函数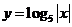 的图像交点个数是
的图像交点个数是
A.2 B.
第Ⅱ卷 (非选择题 共95分)
(用0.
12.设 ,则
,则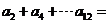 _________________.
_________________.
14.一个无穷等比数列的公比为q,满足0<q<l,前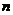 项和为
项和为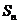 ,且它的第4项与第8项之和等与
,且它的第4项与第8项之和等与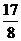 ,第5项与第7项之积等与
,第5项与第7项之积等与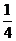 ,则
,则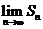 =_________________。
=_________________。
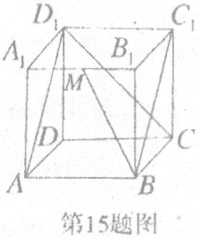
15.如图,正方体ABCD―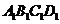 的棱长为1,M是
的棱长为1,M是 的中点,则下列四个命题:
的中点,则下列四个命题:
 ①直线
①直线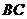 与平面
与平面 所成的角等于45°;
所成的角等于45°;
②四面体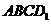 在正方体六个面内的摄影图形面积的最小值为
在正方体六个面内的摄影图形面积的最小值为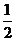 ;
;
③点M到平面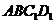 的距离是
的距离是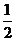 ;
;
④BM与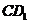 所成的角为
所成的角为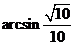 ,其中真命题的序号是____________________。
,其中真命题的序号是____________________。
16.(本小题满分12分)
在周长为6的△ABC中,∠A、∠B 、∠C所对的边分别为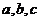 ,若
,若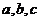 成等比数列;
成等比数列;
(1)求B的取值范围;
(2)求△ABC的面积S的最大值;
(3) 当△ABC的面积S最大时,过△ABC的重心G作直线交边AB于M,交边AC与N,设∠AGM=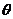 ,
,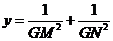 试证:
试证: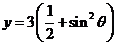 。
。
17.(本小题满分14分)
如图,在四棱锥P-ABCD中,PB⊥底面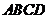 ,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
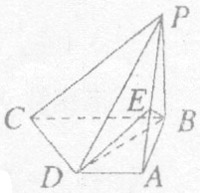 (1)求异面直线PA与CD所成的角;
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A-BE-D的大小。
18.(本小题满分12分)
一次智力竞赛中,共分三个环节:选答、抢答、风险选答,在第一环节“选答”中.每个选手可以从6道题(其中4道选择题,2道操作题)中任意选3道题作答,答对每道题可得100分;在第二环节“抢答”中,一共为参赛选手准备了5道抢答题.答对一道得1 00分,在每一道题的抢答中,每位选手抢到的概率是相等的;在第三环节“风险选答”中,一共为选手准备了A、B、C 三类不同的题目,选手每答对一道A类、B类、C类的题目将分别得到300分、200分、100分,但如果答错,则相应地要扣除300分、200分、100分.而选手答对一道A类、B类、C类题目的概率分别是0.6、0.7、0.8,现有甲、乙、丙三位选手参加比赛,试求:
(1)乙选手在第一环节中,至少选中一道操作题的概率;
(2)甲选手在第二环节中抢到的题数多于乙选手而不多于丙选手的概率;
(3)在第三环节中,就每道题而言,丙选手选择哪类题目得分的期望值更大.
19.(本小题满分I 3分)
某容器中装有浓度为r%的溶液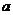 ml,倒出
ml,倒出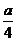 ml后,再倒入浓度为p%的溶液
ml后,再倒入浓度为p%的溶液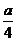 ml(P>r)搅匀,如此反复操作,设第n次操作后溶液的浓度为
ml(P>r)搅匀,如此反复操作,设第n次操作后溶液的浓度为 %,第n+1次操作后溶液的浓度为
%,第n+1次操作后溶液的浓度为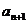 %.
%.
(1)求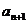 与
与 的关系式;
的关系式;
(2)求第n次操作后溶液的浓度 %;
%;
(3)记: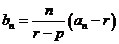 。求数列
。求数列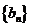 的前n项和
的前n项和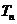 。
。
20.(本小题满分14分)
已知函数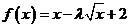 在
在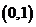 上单调递减,
上单调递减,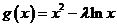 在
在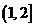 上单调递增.
上单调递增.
(1)求实数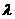 的值;
的值;
(2)求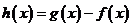 的最小值;
的最小值;
(3)当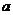 >1时,若
>1时,若 ≥
≥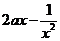 在
在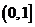 上恒成立,求
上恒成立,求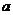 的取值范围.
的取值范围.
21.(本小题满分I 4分)
已知两定点A(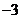 ,0),B(3,0),动圆M与直线AB相切于点N.且
,0),B(3,0),动圆M与直线AB相切于点N.且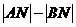 =4,现分别过点A、B作动圆M的切线(异于直线AB),两切线相交于点P.
=4,现分别过点A、B作动圆M的切线(异于直线AB),两切线相交于点P.
(1)求动点P的轨迹方程;
(2)若直线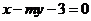 截动点P的轨迹所得的弦长为5,求m的值;
截动点P的轨迹所得的弦长为5,求m的值;
(3)设过轨迹上的点P的直线与两直线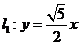 ,
,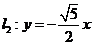 分别交于点
分别交于点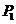 ,
,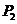 ,且点
,且点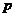 分有向线段
分有向线段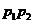 所成的比为
所成的比为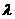 (
(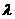 >0),当
>0),当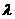 ∈
∈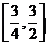 时,求
时,求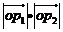 的最小值与最大值。
的最小值与最大值。
2009届安徽高考信息交流试卷

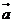 =(1,1),
=(1,1),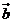 =(1,-1),
=(1,-1),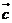 =(
=(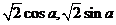 )(
)( 满足
满足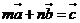 ,则
,则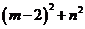 的最大值为_____________.
的最大值为_____________.