1.(1＋x)²ⁿ(n∈N^*)的展开式中，系数最大的项是(　)

A.第＋1项 　B. 第n项　　　 C.第n＋1项 　D.第n项与第n＋1项

2.若集合A ＝{x|ax²－2x＋1＝0}有两个不同元素.则实数a的最大整数解是 (　)

A.1  B.0  C.－1  D.－2.

3.已知函数f(x)＝，则函数f[f(x)]的定义域为(　)

A.{x|x≠1} 　　　  B.{x|x≠2}

C.{x|x≠1或x≠2}　  D.{x|x≠1且x≠2}

4.(理)极限 的值是(　)

A.  B.－  C.  D.－

(文)已知函数f(x)的导数为f′(x)，若f′(x)<0(a <x <b)且f(b)>0，则在(a ，b)内必有(　)

A.f(x)＝0        B.f(x)>0         C.f(x)<0  D.不能确定

5.(理)北京奥组委在29届奥运会举行前夕宣布，将在本次奥运会推出71款贵金属奥运特许商品新品，主要走中低端路线，一些中低价位的镀金纪念章售价仅为66元至196元.此次推出的新品包括18款常规镀金银类产品、40款中低价位为主的金银类产品及13款珍藏系列金银、金玉新工艺纪念章和摆件.为了调查它们的质量，需从这三类产品中抽取一个容量为36的样本，最适合的抽取样本的方法是(　)

A.简单随机抽样

B.系统抽样

C.分层抽样

D.先从珍藏系列金银、金玉新工艺纪念章和摆件中排除1款，再分层抽样

(文)某网站欲调查网民对当前网页的满意程度，在登录的所有网民中，收回有效帖子共50000份，其中持各种态度的份数如下表所示.

很满意

满意

一般

不满意

10800

12400

15600

11200

为了了解网民的具体想法和意见，以便决定如何更改才能使网页更完美，打算从中抽选500份，为使样本更具有代表性，则在“满意”态度中要抽取(　)

A.108  B.124  C.156  D.112

6.(理) 函数 f(x)＝2x²－lnx 的单调增区间是(　)

A.(－ ,0)和(，＋∞)  B.(0，)

 C.(，＋∞)  D.(－，0)和(0，)

(文)曲线f(x)＝x³＋x－2在p₀点处的切线平行于直线y＝4x－1，则p₀点的坐标为 (　)

A.(－1,0)  B.(0，－2)

C.(－1，－4)或(1,0)  D.(1,4)

7.二次函数f(x)＝ax²＋bx＋c 对一切x∈R，满足f(1－x)＝f(1＋x)，且f(－1)<0，f(0)>0，则(　)

A.a＋b＋c<0       B.b<a＋c         C.c<2b         D.a，b，c均大于0

8.(理)同时抛掷5枚均匀的硬币80次，设5枚硬币正好出现2枚正面向上，3枚反面向上的次数为ξ，则ξ的数学期望是(　)

A.20  B.25         C.30      D.40

(文)已知一组数据x₁，x₂，x₃，x₄，x₅的平均数是＝ 2，方差是，那么另一组数据

3x₁－2，　3x₂－2，　3x₃－2，　3x₄ －2，　3x₅－2的平均数和方差分别为(　)

A.2，  B.2,1  C.4，  D.4,3

9.若不等式x⁴－4x³>2－a对于实数x∈[－1,4]恒成立，则实数a的取值范围是(　)

A.[29，＋∞)  B.(29，＋∞)  C.(－∞，－27)  D.(－25，＋∞)

10.设命题p：不等式()^x＋4>m>2x－x²对一切实数x恒成立；命题q：函数

f(x)＝－(7－2m)^x是R上的减函数.若命题p或q为真命题，命题p且q为假命题，则实数m的取值范围是(　)

A  (1 ,4]        B.[3 ,4]∪(－∞，1)

C.[3 ,4]∪(－∞，1]       D.(－∞，4]

11.已知f(x)是定义在R上的偶函数，对任意的x∈R都有f(x＋4)＝f(x)＋f(2)成立.若f(0)＝0，f(1)＝2，则f(1) ＋ f(2)＋f(3)＋…＋f(2007)的值等于(　)

A.2007             B.2008                    C.2009  D.2010

12.(理)已知实数A＝ (1≤m≤2). 则实数A的取值范围是 (　 ).

A.[7－4，2]  B.[，2]  C.[，2]  D.[，]

(文) 已知实数A ＝ ＋(1≤m≤2).则实数A的取值范围是 (　)

A.[0，]  B.[1，]  C.[，1]  D.[0,1]

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

第Ⅱ卷(非选择题　共90分)

13.(理) 已知f(x)＝ax²＋bx，a・b≠0，且f(x₁)＝f(x₂)＝2008.则f(x₁＋x₂)＝　　　　.

(文) 2log₃2－log₃＋log₃8＋5^－log₅³＝　　　　　　.

14.(理)从1,2,3，…，20，这20个数中任取三个数.则这三个数的和能被3整除的概率是　　　　.

(文)在编号为1,2,3，…，n的n张奖券中，采取不放回方式抽奖，若1号为获奖号码，则在第k次(1≤k≤n)抽签时抽到1号奖券的概率为　　　　.

15.某路段检查站监控录象显示，在某时段内，有1000辆汽车通过该站，现在随机抽取其中的200辆汽车进行车速分析，分析的结果表示为右图的频率分布直方图，则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有　　　　辆.

16.若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为y＝x²，值域为{1,4}的“同族函数”共有　　　　.

17.(本小题满分10分)

　　已知奇函数f(x)＝

(1)求实数m的值，并在给出的直角坐标系中画出函数

y＝f(x)的图象；

(2)若函数f(x)在区间[－1，|a|－2]上单调递增，试

确定a的取值范围.

18.(本小题满分12分)

已知f(x)＝－3x²＋a(6－a)x＋b.

(1)解关于a的不等式f(1)>0；

(2)当不等式f(x)>0的解集为(?1,3)时，求实数a，b的值.

19.(本小题满分12分)

　　(理)有A、B、C、D四个城市，它们都有一个著名的旅游点，依次记为a，b，c，d，把A、B、C、D和a，b，c，d分别写成左右两列，现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来，构成“一一对应”.已知每连对一个得2分，连错得0分.

(1)求该爱好者得分的分布列； 

(2)求该爱好者得分的数学期望.

　　(文)已知7件产品中有4件正品和3件次品.

(1)从这7件产品中一次性随机抽出3件，求抽出的产品中恰有1件正品数的概率；

(2)从这7件产品中一次性随机抽出4件，求抽出的产品中正品件数不少于次品件数的概率.

20.(本小题满分12分)

　　(理)已知函数f(x)＝－(x≤－1)，数列{a_n}中，a₁＝－1，a_n＝f^－1(a_n－1)(n＝2,3,4，…).

(1)求a_n，并加以证明；

(2)求 .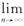

　　(文)某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆，出厂价为13万元/辆，年销售量为5000辆.本年度为适应市场需求，计划提高产品档次，适当增加投入成本，若每辆车投入成本增加的比例为x(0＜x＜1)，则出厂价相应提高的比例为0.7x，年销售量也相应增加.已知年利润＝(每辆车的出厂价－每辆车的投入成本)×年销售量.

(1)若年销售量增加的比例为0.4x，为使本年度的年利润比上年度有所增加，则投入成本增加的比例x应在什么范围内？

(2)年销售量关于x的函数为y＝3240(－x²＋2x＋)，则当x为何值时，本年度的年利润最大？最大利润为多少？

21.(本小题满分12分)

　　(理)已知实数a为整数.函数f(x)＝x³－2ax²－3a²x在区间(－1,1)上有极大值，在区间(1，＋∞)上有极小值，函数g(x)＝ax³＋(a＋b)x²－b，若g(x)≥f(x)在区间[－1,2]恒成立.

(1)求实数a的值；

(2)求实数b的取值范围.

　　 (文)已知函数f(x)＝－x³＋ax²＋bx＋c图像上的点P(1，－2)处的切线方程为y＝－3x＋1.

(1)若函数f(x)在x＝－2时有极值，求f(x)的表达式；

(2)函数f(x)在区间[－2,0]上单调递增，求实数b的取值范围.

22.(本小题满分12分)

　　设n为正整数，规定：f_n(x)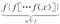＝，已知f(x)＝ .

(1)解不等式f(x)≤x；

(2)设集合A＝{0,1,2}，对任意x∈A，证明f₃(x)＝x；

(3)求f₂₀₀₇()的值；

(4)(理)若集合B＝，证明B中至少包含8个元素.