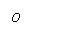1. 已知i是虚数单位,实数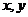 满足
满足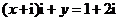 ,则
,则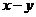 的值为
( )
的值为
( )
A.-1 B.
2.
计算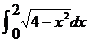 的结果是
( )
的结果是
( )
A. 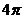 B.
B.
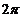 C.
C.
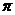 D.
D.
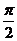
3. 对某校400名学生的体重(单位: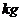 )进行统计,得到如图所示的频率分布直方图,则
)进行统计,得到如图所示的频率分布直方图,则
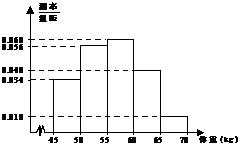 学生体重在60
学生体重在60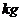 以上的人数为
( )
以上的人数为
( )
A. 200
B. 100
C. 40
D. 20
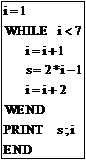 4. 右边的程序运行后,输出的结果为
( )
4. 右边的程序运行后,输出的结果为
( )
A. 13,7
B. 7,4
C. 9,7
D. 9,5
5. 已知椭圆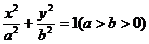 的焦点分别为
的焦点分别为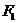 、
、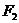 ,
,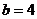 ,
,
离心率为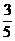 .过
.过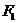 的直线交椭圆于A、B两点,则
的直线交椭圆于A、B两点,则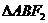 的周长为 ( )
的周长为 ( )
A. 10 B. 12 C. 16 D. 20
6. 已知函数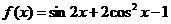 ,将
,将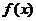 的图象上各点的横坐标伸长到原来的2倍,
的图象上各点的横坐标伸长到原来的2倍,
纵坐标不变,再将所得图象向右平移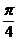 个单位,得到函数
个单位,得到函数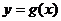 的图象,则
的图象,则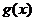 的解
的解
析式为 ( )
A. 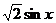 B.
B.
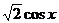 C.
C.
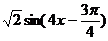 D.
D.
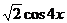 .
.
7. 下列说法正确的是 ( )
A. 函数 的图象的一条对称轴是直线
的图象的一条对称轴是直线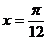
B. 若命题P:“存在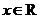 ,
,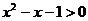 ”,则命题P的否定:“任意
”,则命题P的否定:“任意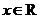 ,
,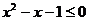 ”C. 若
”C. 若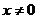 ,则
,则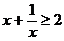
D.
“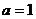 ”是“直线
”是“直线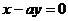 与直线
与直线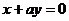 互相垂直”的充要条件
互相垂直”的充要条件
8. 设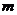 、
、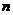 是两条不同直线,
是两条不同直线, 、
、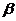 、
、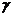 是三个不同平面,给出下列四个命题:
是三个不同平面,给出下列四个命题:
①若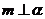 ,
,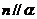 ,则
,则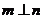 ②若
②若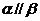 ,
,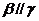 ,
,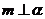 ,则
,则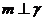
③若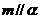 ,
,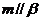 ,则
,则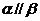 ④若
④若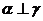 ,
,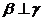 ,则
,则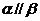
其中正确命题的序号是 ( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
9. 对任意两个正整数m、n定义某种运算+: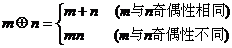 ,则集合
,则集合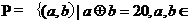 N
N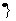 中元素的个数为 ( )
中元素的个数为 ( )
A. 21 B. 22 C. 23 D. 24
 10. 把正整数按一定的规则排成了如图所示的三角形数表.设
10. 把正整数按一定的规则排成了如图所示的三角形数表.设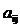 (i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如
(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如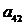 =8.
=8.
若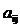 =2009,则i与j的和为( )
=2009,则i与j的和为( )
A. 105 B. 106
C. 107 D. 108
第Ⅱ卷(非选择题 共100分)
11. 袋中有3个黑球,1个红球.从中任取2个,取到一个黑球得0分,取到一个红球得2
分,则所得分数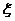 的数学期望
的数学期望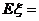 .
.
12. 已知二项式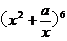 的展开式中的常数项为15,则实数
的展开式中的常数项为15,则实数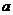 为
.
为
.
13. 设向量a,b满足| a-b |=2,| a |=2,且a-b与a的夹角为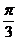 ,则| b |=
.
,则| b |=
.
14. 已知函数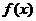 是定义在R上的奇函数,当x
是定义在R上的奇函数,当x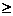 0时,
0时,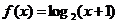 . 若
. 若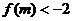 ,
,
则实数m的取值范围是 .
15. 对任意正整数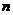 ,定义
,定义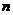 的双阶乘
的双阶乘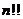 如下:
如下:
当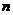 为偶数时,
为偶数时,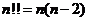
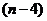
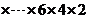 ;
;
当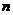 为奇数时,
为奇数时,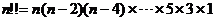 .
.
现有四个命题:
①(2009!!)・(2008!!)=2009!; ② 2008・2008!!=2009!!- 2008!!;
③ 2009!!的个位数字为5; ④(a+b)!! = a!!+b!!(a、b N*)
N*)
其中所有正确命题的序号是 .
16.(本小题满分13分)
已知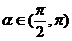 ,且
,且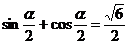 .
.
(Ⅰ)求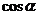 的值;
的值;
(Ⅱ)若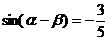 ,
,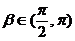 ,求cos
,求cos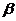 的值.
的值.
17.(本小题满分13分)
如图,在体积为1的三棱柱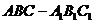 中,侧棱
中,侧棱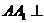 底面
底面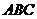 ,
,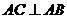 ,
,
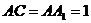 ,
,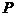 为线段
为线段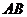 上的动点.
上的动点.
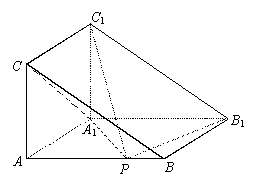 (Ⅰ)求证:
(Ⅰ)求证: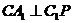 ;
;
(Ⅱ)当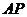 为何值时,二面角
为何值时,二面角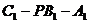 的
的
大小为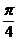 ?
?
18. (本小题满分13分)
近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车容影响了市容市
貌. 今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那
么一年内在该洗车行洗车的平均辆次是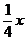 ,该洗车行每年的其他费用是20000元. 问:
,该洗车行每年的其他费用是20000元. 问:
洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
(注:洗车行A买一台污水净化器就能满足洗车净水需求)
19.(本小题满分13分)
已知抛物线C: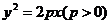 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
 (Ⅰ)求抛物线C的方程;
(Ⅰ)求抛物线C的方程;
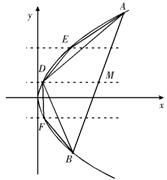
(Ⅱ)设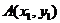 ,
,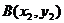 是抛物线C上任意两点,且
是抛物线C上任意两点,且
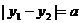 (
(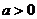 ,且
,且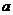 为常数). 过弦AB的中点
为常数). 过弦AB的中点
得到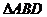 ,求证:
,求证: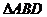 的面积为定值;
的面积为定值;
(Ⅲ)在(Ⅱ)的条件下,分别过弦AD、BD的中点作垂直于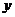
轴的直线依次交抛物线于点E、F,连结AE、DE和BF、
DF,得到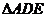 和
和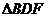 ,并按此方法继续下去. 若设
,并按此方法继续下去. 若设
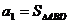 ,
,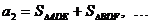 ,
,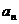 是第n次操作时得到的
是第n次操作时得到的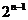 个三角形面积
个三角形面积
的和,记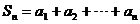 ,求证:
,求证: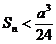 .
.
20.(本小题满分14分)
设函数 (
(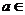 R).
R).
(Ⅰ)当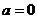 时,求
时,求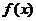 的极值;
的极值;
(Ⅱ)当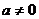 时,求
时,求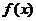 的单调区间;
的单调区间;
(Ⅲ)当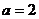 时,对于任意正整数n,在区间
时,对于任意正整数n,在区间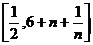 上总存在m+4个数
上总存在m+4个数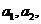
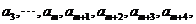 使得
使得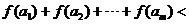
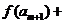
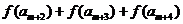 成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵P=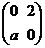 ,Q=
,Q=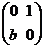 ,若矩阵PQ对应的变换把直线
,若矩阵PQ对应的变换把直线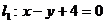 变为直线
变为直线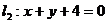 ,求
,求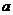 、
、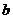 的值.
的值.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线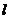 的极坐标方程是
的极坐标方程是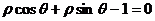 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,椭圆C的参数方程是
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,椭圆C的参数方程是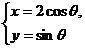 (
(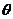 为参数),求直线
为参数),求直线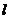 和椭圆C相交所成弦的弦长.
和椭圆C相交所成弦的弦长.
(3)(本小题满分7分)选修4-5:不等式选讲
已知实数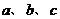 满足
满足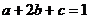 ,
,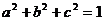 ,求证:
,求证: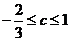 .
.
2009年龙岩市普通高中毕业班单科质量检查