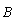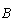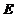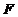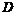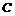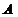1.函数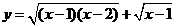 的定义域为 .
的定义域为 .
 2.已知复数与
2.已知复数与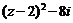 均为纯虚数,则等于 .
均为纯虚数,则等于 .
3.已知向量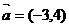 ,向量满足∥,且
,向量满足∥,且 ,则=
。
,则=
。
4.在等比数列{an}中,已知a4+a10=10,且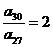 ,则= .
,则= .
5.已知命题:“ ,使x2+2x+a≥
,使x2+2x+a≥
范围是 .
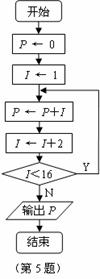
6.如图,程序执行后输出的结果为 .
7.下列命题正确的序号是_____ .
(其中l,m表示直线, 表示平面)
表示平面)
(1)若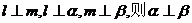 ; (2)若
; (2)若 ;
;
(3)若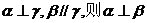 ;
(4)若
;
(4)若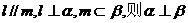
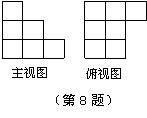 8. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
8. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
则它的体积的最大值与最小值之差为 .
9.已知 ,则当mn取得最小值时,椭圆
,则当mn取得最小值时,椭圆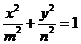 的离心率为
.
的离心率为
.
10.对任意两个集合A、B,定义: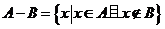 ,
,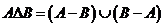 ,设
,设 ,
, ,则
,则
11.若 ,且当
,且当 时,恒有
时,恒有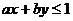 ,则以,b为坐标点
,则以,b为坐标点 所形成的平面区域的面积等于 .
所形成的平面区域的面积等于 .
12.已知两个不共线的向量,的夹角为,且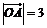 .若点M在直线OB上,且
.若点M在直线OB上,且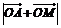 的最小值为,则的值为 .
的最小值为,则的值为 .
13.设函数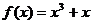 ,若
,若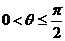 时,
时, 恒成立,则实数的取值范围是
_
.
恒成立,则实数的取值范围是
_
.
14.f(x)是定义在(0,+∞)上的非负可导函数,且满足 ,对任意正数a、b,若a<b,则
,对任意正数a、b,若a<b,则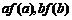 的大小关系为
.
的大小关系为
.
15.(本题满分14分)在△ABC中,角A、B、C的对边分别为a、b、c,若
(1)判断△ABC的形状;
(2)若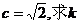 的值.
的值.
16.(本题满分14分)一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.
(1)求证:PB//平面AEC;
17.(本题满分15分)已知圆A: 与轴负半轴交于B点,过B的弦BE与轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
与轴负半轴交于B点,过B的弦BE与轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
(1)求椭圆的方程;
(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.
18.(本题满分15分)
如图所示,一条直角走廊宽为
⑴若平板车卡在直角走廊内,且∠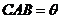 ,试求平板面的长 (用表示);
,试求平板面的长 (用表示);
⑵若平板车要想顺利通过直角走廊,其长度不能超过多少米?
19.(本题满分16分)已知数列的前n项和为,点 在直线
在直线 上.数列满足:
上.数列满足:
 ,且
,且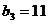 ,前9项和为153.
,前9项和为153.
(1)求数列,的通项公式;
(2)设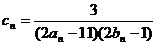 ,数列的前n项和为,求使不等式
,数列的前n项和为,求使不等式 对一切
对一切 都成立的最大正整数的值;
都成立的最大正整数的值;
(3)设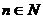 *,
*, 问是否存在
问是否存在 ,使得
,使得 成立?若存在,求出的值;若不存在,请说明理由.
成立?若存在,求出的值;若不存在,请说明理由.
20.(本题满分16分)函数 .
.
(1)试求f(x)的单调区间;
(2)当a>0时,求证:函数f(x)的图像存在唯一零点的充要条件是a=1;
(3)求证:不等式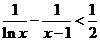 对于
对于 恒成立.
恒成立.
数学附加题
考试时间:30分钟 满分40分
分.每小题10分,共20分.解答时应写出文字说明、证明过程或演算过程.
 1.(选修4一l:几何证明选讲)
1.(选修4一l:几何证明选讲)
如图,圆O的直径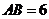 ,C为圆周上一点,
,C为圆周上一点, ,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E。求
,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E。求 的度数与线段AE的长。
的度数与线段AE的长。
2.(选修4―2:矩阵与变换)
已知二阶矩阵A的属于特征值-1的一个特征向量为,属于特征值3的一个特征向量为,求矩阵A.
3.(选修4―4:坐标系与参数方程)
已知直线和参数方程为
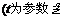 ,是椭圆
,是椭圆 上任意一点,求点到直线的距离的最大值.
上任意一点,求点到直线的距离的最大值.
4.(选修4―5:不等式选讲)
已知f(x)=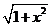 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
(1)求证: | f(x1)-f(x2)|≤| x1-x2| (2)若a2+b2=1,求证:f(a)+f(b) ≤.
选做题一:
选做题二:
 5. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.设复数
5. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.设复数 (i是虚数单位)。
(i是虚数单位)。
(1)求事件“为实数”的概率;
(2)求事件“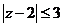 ”的概率。
”的概率。
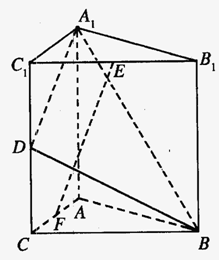
6. 如图,直三棱柱A1B
(1)求与平面A
(2) 求二面角B―A1D―A的平面角的正切值;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
江苏省通州市2009届高三第六次调研测试



 , 则为何值时,PA平面BDF? 并求此时几何体F―BDC的体积.
, 则为何值时,PA平面BDF? 并求此时几何体F―BDC的体积.