1.已知集合M={y|y=x2,x∈R},N={y|y2≤2,y∈Z},则M∩N= ▲ .
2.在复平面内,复数 对应的点与原点之间的距离是 ▲ .
3.已知命题p:函数y=lgx2的定义域是R,命题q:函数y=的值域是正实数集,给出命题:①p或q;②p且q;③非p;④非q.其中真命题有 ▲ 个.
4.已知数列{an}是等差数列,a4=7,S9=45,则过点P(2,a3),Q(4,a6)的直线的斜率
 等于 ▲ .
等于 ▲ .
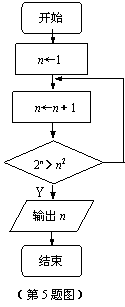
5.右边的流程图最后输出的n的值是 ▲ .
6.若x,y满足约束条件
|
1.已知集合M={y|y=x2,x∈R},N={y|y2≤2,y∈Z},则M∩N= ▲ .
2.在复平面内,复数 对应的点与原点之间的距离是 ▲ .
3.已知命题p:函数y=lgx2的定义域是R,命题q:函数y=的值域是正实数集,给出命题:①p或q;②p且q;③非p;④非q.其中真命题有 ▲ 个.
4.已知数列{an}是等差数列,a4=7,S9=45,则过点P(2,a3),Q(4,a6)的直线的斜率
 等于 ▲ .
等于 ▲ .
5.右边的流程图最后输出的n的值是 ▲ .
6.若x,y满足约束条件
|