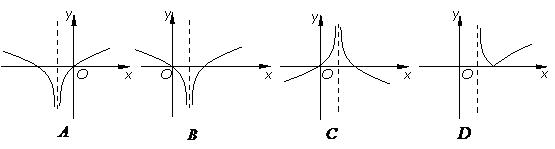1.设集合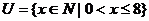 ,
,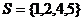 ,
,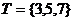 ,则
,则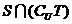 =
=
 .
.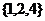
 .
.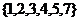
 .
.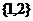
 .
.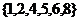
2. 已知复数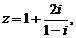 则
则 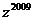 的值为
的值为
 .
.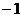
 .
.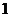
 .
.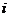
 .
.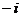
3.正项数列{an}成等比数列,a1+a2=3,a3+a4=12,则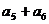 的值是
的值是
 . -24
. -24
 . 21
. 21
 . 24
. 24  . 48
. 48
4.函数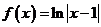 的图像大致形状是
的图像大致形状是
5.在四边形ABCD中,“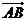 =
=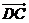 ”是“四边形ABCD为梯形”的
”是“四边形ABCD为梯形”的
 .充分不必要条件
.充分不必要条件  .必要不充分条件
.必要不充分条件  .充要条件
.充要条件  .既不充分也不必要条件
.既不充分也不必要条件
6某校根据新课程标准改革的要求,开设数学选修4系列的10门课程供学生选修,其中4―1,4―2,4―4三门由于上课时间相同,所以至多选一门,根据学分制要求,每位同学必须选修三门,则每位同学不同的选修方案种数是
 .
.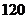 ;
;  .
.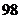 ;
;  .
.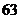 ;
;  .
.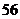 ;
;
7.一个正方体的顶点都在球面上,它的棱长为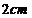 ,则球的表面积是
,则球的表面积是
 .
.
 .
.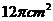
 .
.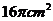
 .
.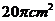
8.已知函数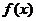 是定义在
是定义在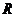 上的奇函数,当
上的奇函数,当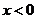 时,
时,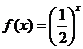 ,那么
,那么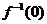 的值为
的值为
 .
.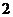
 .
.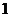
 .
.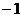
 .
.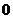
9. 已知抛物线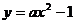 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
 .
.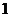
 .
.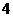
 .
.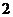
 .
.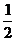
10.已知正三棱锥的侧棱长是底面边长的2倍,则侧棱与底面所成角的余弦值等于
 .
.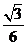
 .
.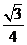
 .
.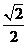
 .
.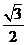
11. 在二项式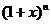 的展开式中,存在系数之比为
的展开式中,存在系数之比为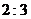 的相邻两项,则指数
的相邻两项,则指数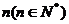 的最小值为
的最小值为
 .6
.6  .5
.5  .4
.4  .3
.3
12.双曲线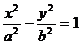
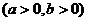 的两个焦点为
的两个焦点为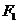 、
、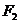 ,若
,若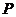 为其上一点,且
为其上一点,且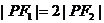 ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为
 .
.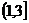
 .
.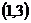
 .
.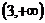
 .
.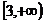
海拉尔二中2009届高三第六次阶段考试试题(理)
第Ⅱ卷(非选择题,共90分)
13. 实数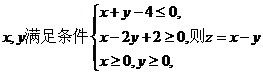 的最大值为________ .
的最大值为________ .
14. 设曲线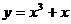 在点
在点 处的切线与直线
处的切线与直线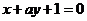 垂直,则
垂直,则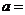 ______.
______.
15. 将圆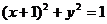 按向量
按向量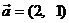 平移后,恰好与直线
平移后,恰好与直线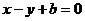 相切,则
相切,则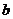 =_______
=_______
16. 在某项测量中,测量结果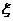 服从正态分布
服从正态分布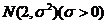 ,若
,若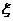 在(0,2)内
在(0,2)内
取值的概率为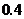 ,则
,则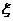 在
在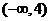 内取值的概率为_______
内取值的概率为_______
17.(本小题满分10分)已知向量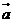 =(sin(
=(sin(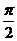 +x),
+x),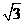 cosx),
cosx),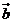 =(sinx, cosx), f(x)=
=(sinx, cosx), f(x)= 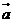 ・
・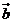 .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果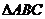 中,满足
中,满足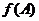 =
=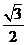 ,求角A的值.
,求角A的值.
18.(本小题满分12分) 某次抽奖活动,有彩票号从0001到1000共1000张彩票,其中彩票号为0123是一等奖,奖金5000元;彩票号后两位数为23的是二等奖,奖金1000元;彩票号尾数为3是三等奖,奖金20元.
(1)某人买了2张彩票,问他获得一等奖或二等奖的概率是多少?(用分数表示)
(2)某人买了1张彩票,求他获得奖金数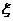 的分布列以及期望
的分布列以及期望
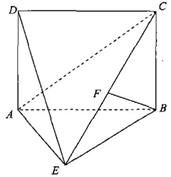 19.(本小题满分12分) 如图,直二面角
19.(本小题满分12分) 如图,直二面角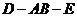 ,四边形
,四边形 是边长为2的正方形,
是边长为2的正方形,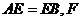 为CE上的点,且
为CE上的点,且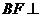 平面
平面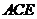 .
.
(1)求证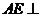 平面
平面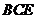 ;
;
(2)求二面角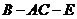 的大小.
的大小.
20.(本小题满分12分) 设数列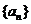 满足:
满足:
(1)令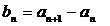 ,求数列
,求数列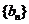 的通项公式;
的通项公式;
(2)求数列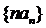 的前
的前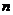 项和
项和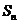 .
. 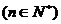
21.(本题12分)椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在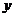 轴上,焦点到相应准线的距离及离心率均为
轴上,焦点到相应准线的距离及离心率均为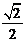 ,直线
,直线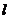 与
与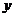 轴交于点
轴交于点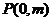 ,与椭圆
,与椭圆 交于相异两点
交于相异两点 ,
,
(1)求椭圆方程;
(2)若 ,求
,求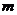 的取值范围.
的取值范围.
22.(本题满分12分) 已知函数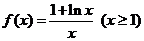
(1)试判断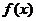 的单调性,并说明理由;
的单调性,并说明理由;
(2)若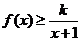 恒成立,求实数
恒成立,求实数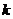 的取值范围;
的取值范围;