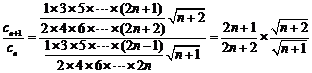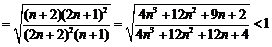1.函数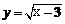 的定义域为______ .
的定义域为______ .
2.设 ,且
,且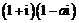 为纯虚数,则
为纯虚数,则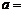 ______.
______.
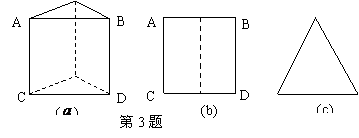
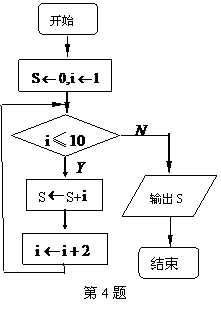 3.如图(
3.如图(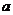 ),直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图(b),(c)所示,则其左视图的面积为_______________.
),直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图(b),(c)所示,则其左视图的面积为_______________.
4.如果执行如图的流程图,那么输出的 .
.
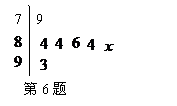 5.已知双曲线
5.已知双曲线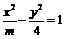 的一条渐近线的方程为
的一条渐近线的方程为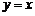 ,则此双曲线两条准线间距离为_____.
,则此双曲线两条准线间距离为_____.
6.如图是某次青年歌手电视大奖赛上一位选手得分的茎叶统计图,
但是有一个数字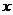 不清晰.根据比赛规则要去掉一个最高分和一个
不清晰.根据比赛规则要去掉一个最高分和一个
最低分.已知所剩数据的平均数为85,则所剩数据的方差为 _____ .
.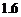
7.利用计算机在区间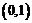 上产生两个随机数
上产生两个随机数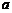 和
和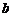 ,则方程
,则方程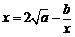 有实根的概率为 .
有实根的概率为 .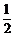
8.已知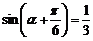 ,则
,则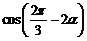 的值等于________.
的值等于________.
9.某单位用3.2万元购买了一台实验仪器,假设这台仪器从启用的第一天起连续使用,第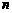 天的维修保养费为
天的维修保养费为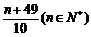 元,若使用这台仪器的日平均费用最少,则一共使用了 天.
元,若使用这台仪器的日平均费用最少,则一共使用了 天.
10.连续2次抛掷一枚骰子(六个面上分别标有数字1,2,3,4,5,6),记“两次向上的数字之和等于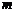 ”为事件
”为事件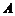 ,则
,则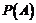 最大时,
最大时,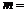 .
.
11. 已知下列两个命题:
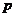 :
: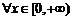 ,不等式
,不等式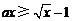 恒成立;
恒成立;
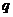 :1是关于x的不等式
:1是关于x的不等式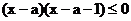 的一个解.
的一个解.
若两个命题中有且只有一个是真命题,则实数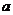 的取值范围是
.
的取值范围是
.
12.定义一个对应法则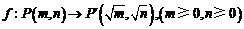 .现有点
.现有点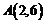 与
与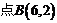 ,点
,点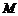 是
是
线段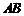 上一动点,按定义的对应法则
上一动点,按定义的对应法则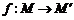 .当点
.当点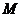 在线段
在线段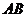 上从点
上从点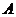 开始运动到点
开始运动到点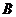 结束时,点
结束时,点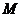 的对应点
的对应点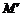 所经过的路线长度为 .
所经过的路线长度为 .
13.设曲线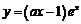 在点
在点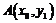 处的切线为
处的切线为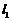 ,曲线
,曲线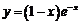 在点
在点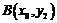 处的切线为
处的切线为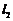 ,若存在
,若存在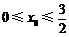 ,使得
,使得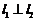 ,则实数
,则实数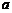 的取值范围是
.
的取值范围是
.
14.数列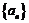 满足
满足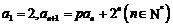 ,其中
,其中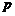 为常数.若存在实数
为常数.若存在实数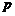 ,使得数列
,使得数列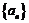 为等差数列或等比数列,则数列
为等差数列或等比数列,则数列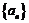 的通项公式
的通项公式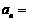 .
.
15.在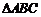 中,角
中,角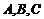 的对边分别为
的对边分别为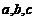 ,且
,且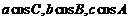 成等差数列.
成等差数列.
⑴求角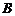 的值;
的值;
⑵若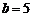 ,求△
,求△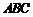 周长的取值范围.
周长的取值范围.
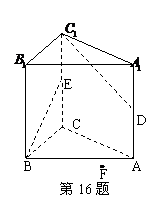 16.已知直三棱柱
16.已知直三棱柱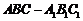 中,
中,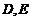 分别为
分别为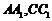 的中点,
的中点,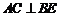 ,点
,点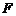 在线段
在线段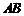 上,且
上,且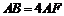 .
.
⑴求证: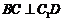 ;
;
⑵若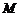 为线段
为线段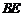 上一点,试确定
上一点,试确定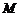 在线段
在线段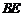 上的位置,
上的位置,
使得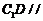 平面
平面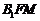 .
.
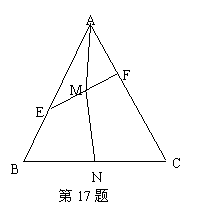 17.如图,在边长为1的正三角形
17.如图,在边长为1的正三角形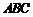 中,
中,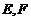 分别是边
分别是边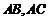 上的点,若
上的点,若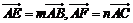 ,
,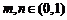 .设
.设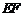 的中点为
的中点为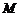 ,
,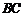 的中点为
的中点为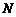 .
.
⑴若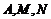 三点共线,求证
三点共线,求证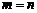 ;
;
⑵若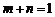 ,求
,求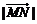 的最小值.
的最小值.
18.已知椭圆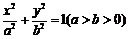 的左、右焦点分别为
的左、右焦点分别为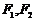 ,其右准线上
,其右准线上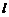 上存在点
上存在点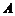 (点
(点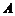 在
在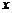 轴上方),使
轴上方),使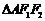 为等腰三角形.
为等腰三角形.
⑴求离心率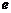 的范围;
的范围;
⑵若椭圆上的点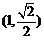 到两焦点
到两焦点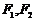 的距离之和为
的距离之和为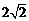 ,求
,求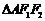 的内切圆的方程.
的内切圆的方程.
19.已知函数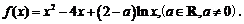
⑴当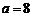 时,求函数
时,求函数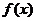 的单调区间;
的单调区间;
⑵求函数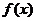 在区间
在区间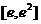 上的最小值.
上的最小值.
20.设数列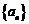 满足
满足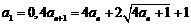 ,令
,令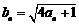 .
.
⑴试判断数列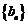 是否为等差数列?并求数列
是否为等差数列?并求数列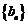 的通项公式;
的通项公式;
⑵令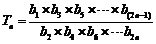 ,是否存在实数
,是否存在实数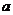 ,使得不等式
,使得不等式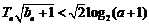 对一切
对一切
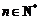 都成立?若存在,求出
都成立?若存在,求出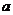 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
⑶比较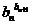 与
与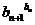 的大小.
的大小.
试题答案
1.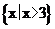 2.
2. 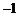 3.
3. 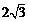 4. 25 5.
4. 25 5. 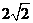 6.
6. 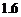
7.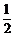 8.
8. 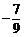 9. 800 10.7 11. a
9. 800 10.7 11. a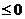 12.
12. 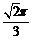 13.
13. 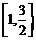 14.
14. 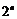
15.⑴因为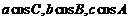 成等差数列,所以
成等差数列,所以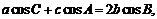 …………2分
…………2分
由正弦定理得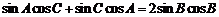 ,即
,即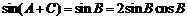 .
.
因为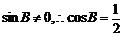 ,又
,又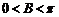 ,所以
,所以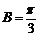 .…………6分
.…………6分
⑵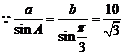 ,
,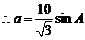 ,同理
,同理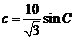 ,…………8分
,…………8分
因为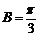 ,所以
,所以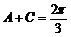 ,
,
所以△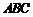 周长
周长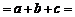
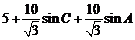
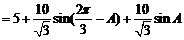
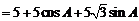
 …………12分
…………12分
因为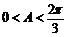 ,所以
,所以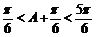 ,所以△
,所以△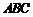 周长的取值范围为
周长的取值范围为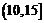 .
…14分
.
…14分
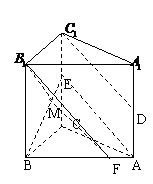 16.⑴由直三棱柱可知
16.⑴由直三棱柱可知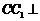 平面
平面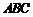 ,所以
,所以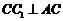 ,…………2分
,…………2分
又因为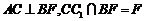 ,
,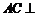 面
面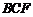 ,
,
故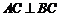 ,
…………4分
,
…………4分
又在直三棱柱中,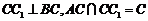 ,
,
故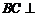 面
面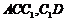 在平面
在平面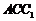 内,所以
内,所以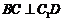 …………6分
…………6分
⑵连结AE,在BE上取点M,使BE=4ME, …………8分
连结FM,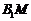 ,F
,F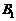 ,在
,在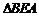 中,由BE=4ME,AB=4AF
中,由BE=4ME,AB=4AF
所以MF//AE, …………12分
又在面AA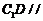 平面
平面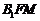 . …………14分
. …………14分
17.⑴由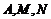 三点共线,得
三点共线,得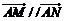 ,
…………………………2分
,
…………………………2分
设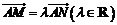 ,即
,即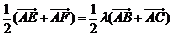 , …………………………4分
, …………………………4分
所以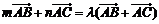 ,所以
,所以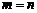 .
…………………………6分
.
…………………………6分
⑵因为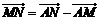 =
=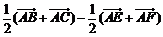
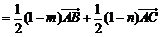 ,
,
又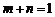 ,所以
,所以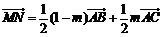 , …………………………10分
, …………………………10分
所以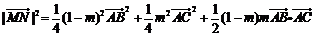
=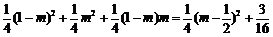
故当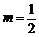 时,
时,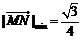 .
…………………………14分
.
…………………………14分
18.⑴由题意有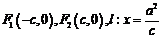 .
…………2分
.
…………2分
设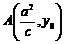 ,由
,由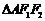 为等腰三角形,则只能是
为等腰三角形,则只能是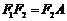 ,又
,又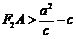 ,
,
即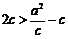 ,所以
,所以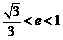 .
…………6分
.
…………6分
⑵由题意得椭圆的方程为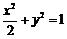 ,其离心率为
,其离心率为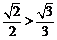 ,此时
,此时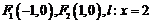 .
.
由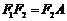 ,可得
,可得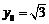 .
…………10分
.
…………10分
设内切圆的圆心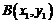 ,
,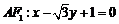 ,
,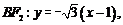
因为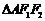 为等腰三角形,所以
为等腰三角形,所以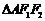 的内切圆的圆心点
的内切圆的圆心点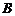 到
到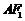 的距离等于点
的距离等于点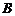 到
到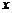 轴的距离,即
轴的距离,即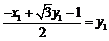 , ①
, ①
由点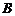 在直线
在直线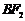 上,所以
上,所以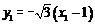 , ②
, ②
由①②可得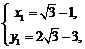
所以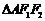 的内切圆的方程为
的内切圆的方程为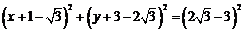 .…………16分
.…………16分
注:本题亦可先用面积求出半径,再求圆的方程.
19.⑴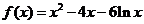 ,
,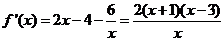 , …………2分
, …………2分
由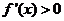 得
得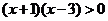 , 解得
, 解得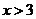 或
或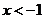 .
.
注意到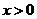 ,所以函数
,所以函数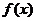 的单调递增区间是
的单调递增区间是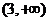 .
.
由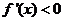 得
得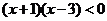 ,解得
,解得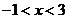 ,
,
注意到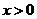 ,所以函数
,所以函数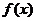 的单调递减区间是
的单调递减区间是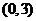 .
.
综上所述,函数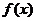 的单调递增区间是
的单调递增区间是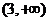 ,单调递减区间是
,单调递减区间是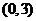 .…………6分
.…………6分
⑵当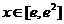 时,
时, 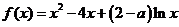 ,所以
,所以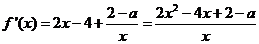 ,
,
设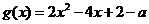 .
.
①当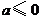 时,有
时,有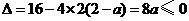 , 此时
, 此时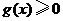 ,所以
,所以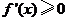 ,
,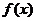 在
在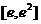 上单调递增.所以
上单调递增.所以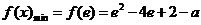 .
…………8分
.
…………8分
②当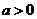 时,
时,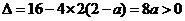 ,
,
令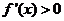 ,即
,即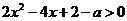 ,解得
,解得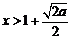 或
或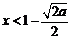 (舍);
(舍);
令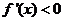 ,即
,即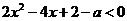 ,解得
,解得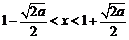 .
.
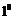 若
若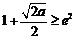 ,即
,即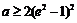 时,
时, 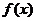 在区间
在区间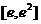 单调递减,
单调递减,
所以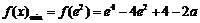 .
.
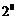 若
若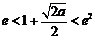 ,即
,即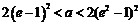 时,
时, 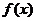 在区间
在区间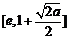 上单调递减,
上单调递减,
在区间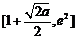 上单调递增,
上单调递增,
所以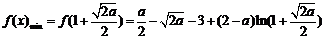 .
.
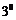 若
若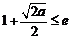 ,即
,即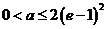 时,
时, 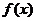 在区间
在区间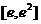 单调递增,
单调递增,
所以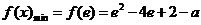 .
…………14分
.
…………14分
综上所述,当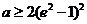 时,
时, 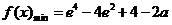 ;
;
当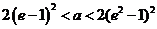 时,
时,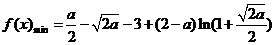 ;
;
当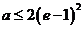 时,
时, 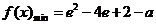 .
…………16分
.
…………16分
20. ⑴由已知得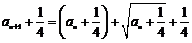 ,
,
即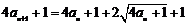 ,
…………2分
,
…………2分
所以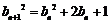 ,即
,即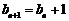 ,
,
又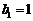 ,所以数列
,所以数列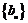 为等差数列,通项公式为
为等差数列,通项公式为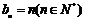 . …………6分
. …………6分
(2)令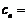
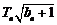 ,由
,由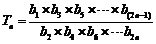 ,得
,得
所以,数列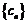 为单调递减数列,
…………8分
为单调递减数列,
…………8分
所以数列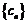 的最大项为
的最大项为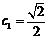 ,
,
若不等式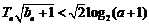 对一切
对一切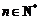 都成立,只需
都成立,只需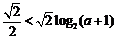 ,解得
,解得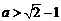 ,
,
又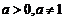 ,所以
,所以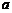 的取值范围为
的取值范围为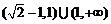 .
…………12分
.
…………12分
(3)问题可转化为比较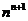 与
与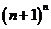 的大小.设函数
的大小.设函数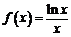 ,所以
,所以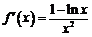 .
.
当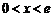 时,
时,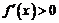 ;当
;当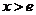 时,
时,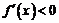 .所以
.所以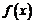 在
在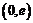 上为增函数;
上为增函数;
在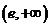 上为减函数.
上为减函数.
当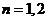 时,显然有
时,显然有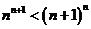 ,
,
当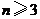 时,
时,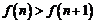 ,即
,即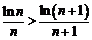 ,所以
,所以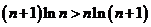 ,
,
即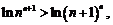 所以
所以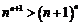 .
.
综上:当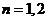 时,
时,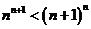 ,即
,即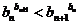 ;
;
当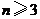 时,
时,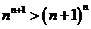 即
即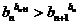 .
…………16分
.
…………16分