1.在等差数列{an}中,如果a4+a7+a10=15,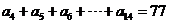 ,
,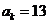 ,那么k等于( )w.w.w.k.s.5.u.c.o.m
,那么k等于( )w.w.w.k.s.5.u.c.o.m
A.14 B.
2 设a>0,b>0,则以下不等式中不恒成立的是 ( )
设a>0,b>0,则以下不等式中不恒成立的是 ( )
A.(a+b)(+)≥4
B.a3+b3≥2ab
3.已知A,B,C,D,E,F,G七个元素排成一排,要求A排在正中间,且B,C相邻,则不同的排法有( )
A.48种 B.96种 C.192种 D.240种
4.设f(x)是定义在R上单调递减的奇函数.若x1+x2>0,x2+x3>0,x3+x1>0,则( )
A.f(x1)+f(x2)+f(x3)<0 B.f(x1)+f(x2)+f(x3)>0
C.f(x1)+f(x2)+f(x3)=0 D.f(x1)+f(x2)>f(x3)
5.已知函数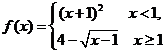 ,则使得f(x)≥1的自变量x的取值范围为( )
,则使得f(x)≥1的自变量x的取值范围为( )
A.(-∞,-2]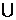 [0,10] B.(-∞,-2]
[0,10] B.(-∞,-2]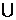 [0,1]
[0,1]
C.(-∞,-2]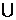 [1,10] D.[-2,0]
[1,10] D.[-2,0]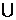 [1,10]
[1,10]
6.在△ABC中,tanA=,cosB=.若最长边为1,则最短边的长为 ( )
A. B. C. D.
7.设 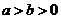 ,那么
,那么 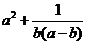 的最小值是( )
的最小值是( )
A.2
B.
8.已知抛物线y2=8x,O是坐标原点,F是焦点,P是抛物线上的点,使得△POF是直角三角形,则这样的P点共有 ( )
A.0个 B.2个 C.4个 D.6个
9.某同学做了10道选择题,每道题四个选择项中有且只有一项是正确的,他每道题都随意地从中选了一个答案.记该同学至少答对9道题的概率为p,则下列数据中与p最接近的是( )
A.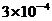 B.
B.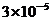 C.
C. D.
D.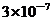
 *10.6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
*10.6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A.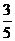 B.
B.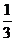 C.
C.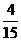 D.
D.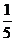
*11.设四棱锥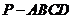 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面 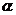 去
去
截此四棱锥,使得截面四边形是平行四边形,则这样的平面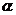 ( )
( )
A.不存在 B.只有1个 C.恰有4个 D.有无数多个
*12.设函数y=f (x)满足f (x+1)=f (x)+1,则方程f (x)=x的根的个数
是 ( )
A.无穷个 B.没有或者有限个 C.有限个 D.没有或者无穷个
第Ⅱ卷(非选择题 共90分)
13. 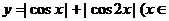 R) 的最小值是
.
R) 的最小值是
.
*14.设集合A={x|log(3-x)≥-2},B={x|≥1},若A∩B=Æ,则实数a的取值范围是_______.
*15.已知函数 ,若
,若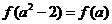 ,则实数a=
.
,则实数a=
.
*16.函数f(x)=xn+(1-x)n,x∈(0,1),n∈N*.记y=f(x)的最小值为an,则a1+a2+…+a6=___.
17.(12分)已知△ABC中,A,B,C的对边分别为a,b,c,且()2=・+・+・.
(Ⅰ)判断△ABC的形状,并求sinA+sinB的取值范围;
*(Ⅱ)若不等式a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a,b,c都成立,求k的取值范围.
18.(12分)一个口袋中装有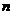 个红球(
个红球( 且
且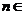 N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用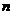 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率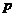 ;
;
(Ⅱ)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ) 记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 .当
.当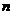 取多少时,
取多少时, 最大?
最大?
19.(12分)定义域均为R的奇函数f(x)与偶函数g(x)满足f(x)+g(x)=10x.
(Ⅰ)求函数f(x)与g(x)的解析式;
(Ⅱ)求函数f(x)的反函数;
(Ⅲ)证明:g(x1)+g(x2)≥
*(Ⅳ)试用f(x1),f(x2),g(x1),g(x2)表示f(x1-x2)与g(x1+x2).
20.(12分)某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100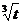 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
21.(12分)设O为坐标原点,A(-,0),点M在定直线x=-p(p>0)上移动,点N在线段MO的延长线上,且满足=.
(Ⅰ)求动点N的轨迹方程,并说明轨迹是什么曲线?
(Ⅱ)若|AN|的最大值≤,求p的取值范围.
22.(14分)已知等差数列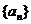 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,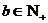 ,且
,且

(Ⅰ)求a的值;
(Ⅱ)若对于任意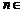 N*,总存在
N*,总存在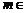 N*,使
N*,使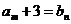 ,求b的值;
,求b的值;
(Ⅲ)甲说:一定存在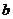 使得
使得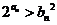 对
对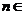 N*恒成立;乙说:一定存在
N*恒成立;乙说:一定存在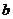 使得
使得 对
对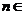 N*恒成立.你认为他们的说法是否正确?为什么?
N*恒成立.你认为他们的说法是否正确?为什么?
2009年厦门市高三质量检查测试二

