1.若集合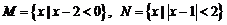 ,则
,则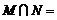 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
A.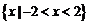 B.
B.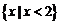 C.
C.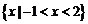 D.
D.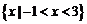
2 数
数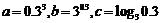 的大小关系是
的大小关系是
A.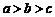 B.
B.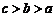 C.
C.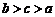 D.
D.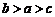
3.条件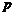 :不等式
:不等式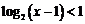 的解;条件
的解;条件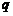 :不等式
:不等式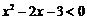 的解,则
的解,则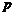 是
是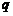 的
的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
4.若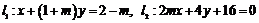 的图象是两条平行直线,则
的图象是两条平行直线,则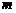 的值是
的值是
A.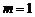 或
或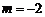 B.
B.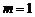 C.
C.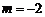 D.
D.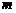 的值不存在
的值不存在
5.在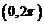 内使
内使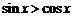 成立的
成立的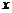 的取值范围是
的取值范围是
A.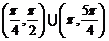 B.
B.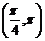 C.
C.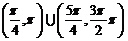 D.
D.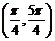
6.若函数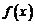 的图象过点
的图象过点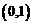 ,则函数
,则函数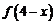 的图象必过点
的图象必过点
A.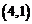 B.
B.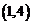 C.
C.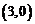 D.
D.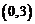
7.在正项等比数列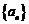 中,
中,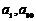 是方程
是方程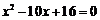 的两个根,则
的两个根,则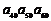 的值为
的值为
A.32 B.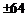 D.256
D.256
8.若函数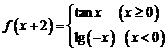 ,则
,则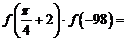
A.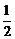 B.
B.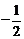 C.2
D.
C.2
D.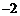
9.已知直线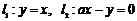 ,其中
,其中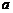 为实数,当这两条直线的夹角在
为实数,当这两条直线的夹角在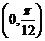 内变动时,
内变动时,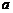 的取值范围是
的取值范围是
A.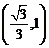 B.
B.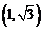 C.
C.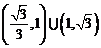 D.
D.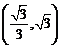
10.已知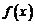 是
是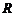 上的增函数,点
上的增函数,点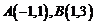 在它的图象上,
在它的图象上,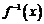 是它的反函数,那么不等式
是它的反函数,那么不等式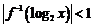 的解集为
的解集为
A.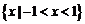 B.
B.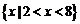 C.
C.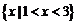 D.
D.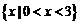
11.已知椭圆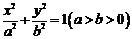 与双曲线
与双曲线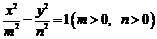 有相同的焦点
有相同的焦点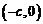 和
和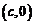 ,若
,若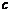 是
是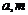 的等比中项,
的等比中项,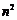 是
是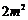 与
与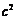 的等差中项,则椭圆的离心率是
的等差中项,则椭圆的离心率是
A.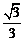 B.
B.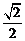 C.
C.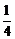 D.
D.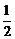
12.某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买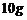 黄金,售货员先将
黄金,售货员先将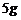 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将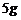 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
A.大于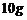 B.小于
B.小于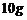 C.大于等于
C.大于等于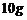 D.小于等于
D.小于等于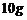
第Ⅱ卷(非选择题 共90分)
13.已知平面向量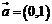 ,
,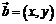 ,若
,若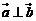 ,则实数
,则实数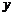 =_______.
=_______.
14.已知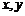 满足约束条件
满足约束条件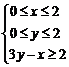 ,则
,则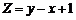 的最大值是______________.
的最大值是______________.
15.已知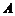 点是圆
点是圆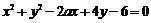 上任一点,
上任一点,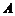 点关于直线
点关于直线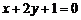 的对称点也在圆上,那么实数
的对称点也在圆上,那么实数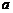 等于____________.
等于____________.
16.已知等差数列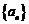 的前
的前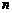 项和为
项和为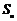 ,若
,若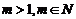 ,且
,且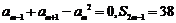 ,则
,则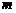 等于_____________.
等于_____________.
17.(12分)在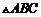 中,
中,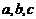 是角
是角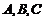 所对的边,
所对的边,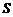 是该三角形的面积,且
是该三角形的面积,且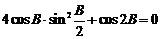 。
。
(Ⅰ)求角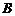 的度数;
的度数;
(Ⅱ)若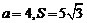 ,求
,求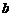 的值。
的值。
18.(12分)已知实数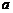 满足不等式
满足不等式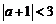 ,解关于
,解关于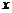 的不等式:
的不等式: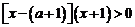
19.(12分)已知函数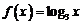 。
。
(Ⅰ)若关于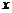 的方程
的方程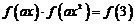 的解都在区间
的解都在区间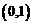 内,求实数
内,求实数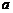 的范围;
的范围;
(Ⅱ)若函数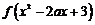 在区间
在区间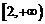 上单调递增,求正实数
上单调递增,求正实数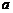 的取值范围。
的取值范围。
20.(12分)某商场只设有超市部、服装部、家电部三个部门,共有200名售货员,计划三个部门日营业额共为55万元,各部门的商品每1万元营业额所需售货员人数如表(1),每1万元营业额所得利润如表(2),若商场预期每日的总利润为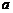 万元,且满足
万元,且满足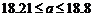 ,又已知商场分配给三个部门的日营业额为正整数万元,问商场怎样分配营业额给三个部门?各部门分别安排多少名售货员?
,又已知商场分配给三个部门的日营业额为正整数万元,问商场怎样分配营业额给三个部门?各部门分别安排多少名售货员?
表(1) 表(2)
部门
每1万元营业额所需人数
超市部
4
服装部
5
家电部
2
部门
每1万元营业额所需人数
超市部
0.3万元
服装部
0.5万元
家电部
0.2万元
21.(12分)设抛物线过定点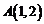 ,且以直线
,且以直线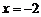 为准线
为准线
(Ⅰ)求抛物线顶点的轨迹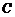 的方程;
的方程;
(Ⅱ)已知点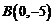 ,轨迹
,轨迹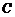 上是否存在满足
上是否存在满足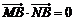 的
的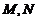 两点?证明你的结论。
两点?证明你的结论。
22.(14分)设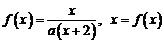 有唯一解,
有唯一解,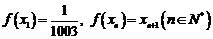 。
。
(Ⅰ)求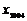 的值;
的值;
(Ⅱ)若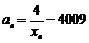 且
且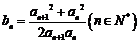 ,求证:
,求证: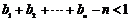
(Ⅲ)是否存在最小整数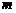 ,使得对于任意
,使得对于任意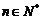 ,有
,有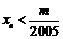 成立,若存在,求出
成立,若存在,求出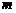 的值;若不存在,说明理由。
的值;若不存在,说明理由。
2009年厦门市高三质量检查测试一

