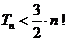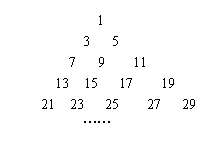(2)该选手在选拔过程中回答过的问题的总个数记为 ,求随机变量
,求随机变量 的分布列与数学期望.
的分布列与数学期望.
18.(本小题满分12分)
如图所示,在直角梯形ABCP中,AP//BC,AP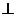 AB, AB=BC=
AB, AB=BC=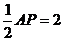 ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将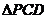 沿CD折起,使得
沿CD折起,使得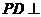 平面ABCD.
平面ABCD.
(1)求证:AP//平面EFG;
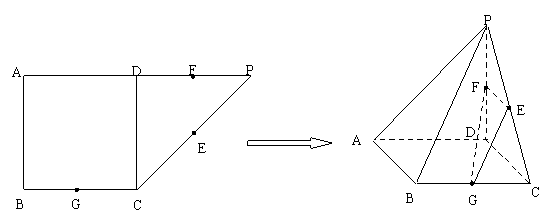 (2) 求
(2) 求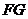 与平面
与平面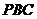 所成角的大小.
所成角的大小.
(3)求二面角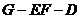 的大小.
的大小.
19.(本小题满分12分)
已知点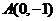 ,点
,点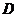 在
在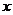 轴上,点
轴上,点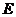 在
在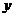 轴正半轴上,点
轴正半轴上,点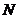 满足
满足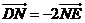 ,
,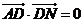 .
.
(1)求动点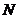 的轨迹
的轨迹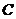 的方程;
的方程;
(2)已知点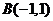 ,若过点
,若过点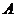 的动直线
的动直线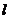 交轨迹
交轨迹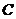 于
于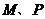 两点,直线
两点,直线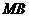 交轨迹
交轨迹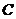 于另一点
于另一点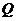 ,证明直线
,证明直线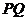 恒过一个定点,并求出定点坐标.
恒过一个定点,并求出定点坐标.
20.(本小题满分13分)
已知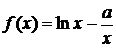 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为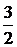 ,求a的值;
,求a的值;
(3)若f(x)<x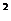 在(1,+
在(1,+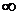 )上恒成立,试求a的取值范围.
)上恒成立,试求a的取值范围.
21.(本小题满分14分)
把正奇数列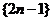 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设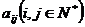 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第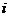 行,从左向右数第
行,从左向右数第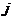 个数.
个数.
(1)若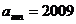 ,求
,求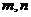 的值;
的值;
(2)已知函数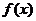 的反函数为
的反函数为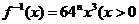 ,
,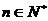 ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第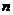 行各数的和为
行各数的和为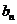 .①求数列
.①求数列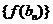 的前
的前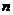 项的和
项的和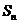 .②令
.②令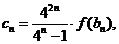
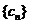 的前
的前 项之积为
项之积为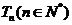 ,求证:
,求证: