1.满足条件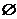
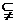 M
M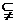 {0,1,2}的集合共有
{0,1,2}的集合共有
A.3个 B.6个 C.7个 D.8个
2.(文)等差数列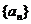 中,若
中,若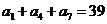 ,
,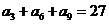 ,则前9项的和
,则前9项的和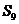 等于
等于
A.66 B.99 C.144 D.297
(理)复数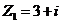 ,
,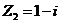 ,则
,则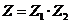 的复平面内的对应点位于
的复平面内的对应点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数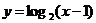 的反函数图像是
的反函数图像是
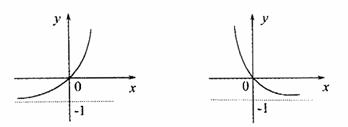
A B
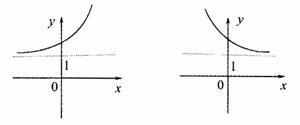
C D
4.已知函数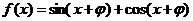 为奇函数,则
为奇函数,则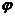 的一个取值为
的一个取值为
A.0 B.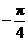 C.
C.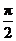 D.
D.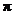
5.从10种不同的作物种子中选出6种放入6个不同的瓶子中展出,如果甲、乙两种种子不能放入第1号瓶内,那么不同的放法共有
A.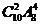 种 B.
种 B.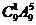 种 C.
种 C.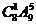 种 D.
种 D.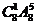 种
种
6.函数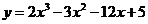 在[0,3]上的最大值、最小值分别是
在[0,3]上的最大值、最小值分别是
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
7.(文)已知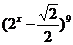 展开式的第7项为
展开式的第7项为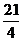 ,则实数x的值是
,则实数x的值是
A.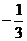 B.-3 C.
B.-3 C.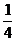 D.4
D.4
(理)已知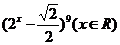 展开式的第7项为
展开式的第7项为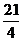 ,则
,则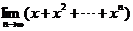 的值为
的值为
A.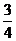 B.
B.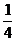 C.
C.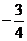 D.
D.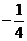
8.过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,则球的表面积是
A.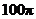 B.
B.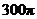 C.
C.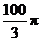 D.
D.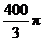
9.给出下面四个命题:
①“直线a、b为异面直线”的充分非必要条件是:直线a、b不相交;
②“直线l垂直于平面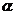 内所有直线”的充要条件是:l⊥平面
内所有直线”的充要条件是:l⊥平面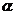 ;
;
③“直线a⊥b”的充分非必要条件是“a垂直于b在平面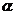 内的射影”;
内的射影”;
④“直线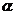 ∥平面
∥平面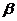 ”的必要非充分条件是“直线a至少平行于平面
”的必要非充分条件是“直线a至少平行于平面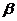 内的一条直线”.
内的一条直线”.
其中正确命题的个数是
A.1个 B.2个 C.3个 D.4个
10.若0<a<1,且函数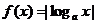 ,则下列各式中成立的是
,则下列各式中成立的是
A.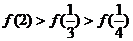 B.
B.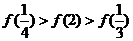
C.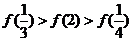 D.
D.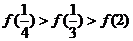
11.如果直线y=kx+1与圆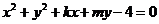 交于M、N两点,且M、N关于直线x+y=0对称,则不等式组:
交于M、N两点,且M、N关于直线x+y=0对称,则不等式组: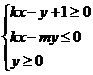 表示的平面区域的面积是
表示的平面区域的面积是
A.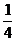 B.
B.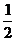 C.1
D.2
C.1
D.2
12.九0年度大学学科能力测验有12万名学生,各学科成绩采用15级分,数学学科能力测验成绩分布图如下图:请问有多少考生的数学成绩分高于11级分?选出最接近的数目
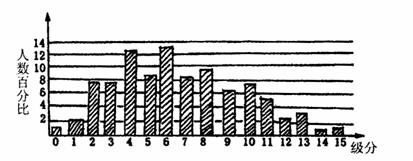
A.4000人 B.10000人 C.15000人 D.20000人
第Ⅱ卷(非选择题,共90分)
13.已知: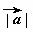 =2,
=2,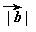 =
=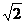 ,
,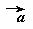 与
与 的夹角为45°,要使
的夹角为45°,要使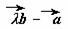 与
与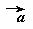 垂直,则
垂直,则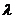 __________.
__________.
14.若圆锥曲线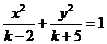 的焦距与k无关,则它的焦点坐标是__________.
的焦距与k无关,则它的焦点坐标是__________.
15.定义符号函数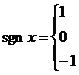
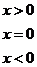 ,则不等式:
,则不等式: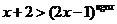 的解集是_______.
的解集是_______.
16.若数列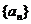 ,
,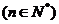 是等差数列,则有数列
是等差数列,则有数列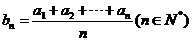 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列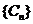 是等比数列,且
是等比数列,且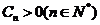 ,则有
,则有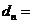 __________
__________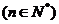 也是等比数列.
也是等比数列.
17.(12分)
一盒中装有20个大小相同的弹子球,其中红球10个,白球6个,黄球4个,一小孩随手拿出4个,求至少有3个红球的概率.
18.(12分)
已知: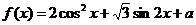 (
(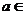 R,a为常数).
R,a为常数).
(1)若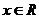 ,求f(x)的最小正周期;
,求f(x)的最小正周期;
(2)若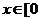 ,
,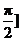 时,f(x)的最大值为4,求a的值.
时,f(x)的最大值为4,求a的值.
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
19甲.(12分)
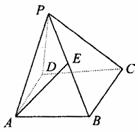 如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点,
如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点,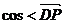 ,
,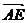
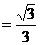 .
.
(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
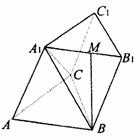 19乙.(12分)如图,三棱柱
19乙.(12分)如图,三棱柱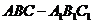 的底面是边长为a的正三角形,侧面
的底面是边长为a的正三角形,侧面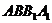 是菱形且垂直于底面,∠
是菱形且垂直于底面,∠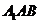 =60°,M是
=60°,M是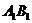 的中点.
的中点.
(1)求证:BM⊥AC;
(2)求二面角 的正切值;
的正切值;
(3)求三棱锥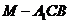 的体积.
的体积.
20.(12分)
已知函数f(x)的图像与函数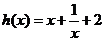 的图像关于点A(0,1)对称.
的图像关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)(文)若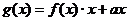 ,且
,且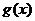 在区间(0,2]上为减函数,求实数a的取值范围;
在区间(0,2]上为减函数,求实数a的取值范围;
(理)若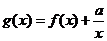 ,且
,且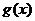 在区间(0,
在区间(0,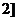 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.
21.(12分)
假设A型进口车关税税率在2002年是100%,在2007年是25%,2002年A型进口车每辆价格为64万元(其中含32万元关税税款).
(1)已知与A型车性能相近的B型国产车,2002年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2007年B型车的价格不高于A型车价格的90%,B型车价格要逐年降低,问平均每年至少下降多少万元?
(2)某人在2002年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带息是否一定够买按(1)中所述降价后的B型车一辆?
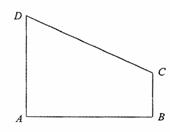
22.(14分)
如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=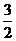 ,BC=
,BC=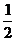 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.
(1)建立适当坐标系,求椭圆C的方程;
(2)(文)是否存在直线l与椭圆C交于M、N两点,且线段MN的中点为C,若存在,求l与直线AB的夹角,若不存在,说明理由.
 (理)若点E满足
(理)若点E满足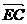
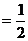
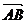 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且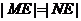 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.

