1.已知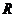 为实数集,
为实数集,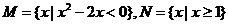 ,则
,则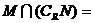 ( ).
( ).
A.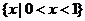 B.
B.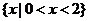 C.
C.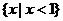 D.
D.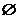
2.设 复数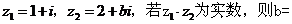 ( )
( )
A.2
B.
3.下列函数中,在区间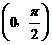 上为增函数且以
上为增函数且以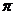 为周期的函数是
为周期的函数是
A.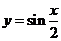 B.
B. 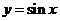 C.
C. 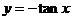 D.
D.
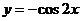
4.给定两个向量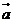 =(3,4)、
=(3,4)、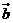 =(2,-1),且(
=(2,-1),且(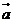 +λ
+λ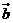 )⊥(
)⊥(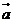 -
-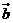 ),则λ=
),则λ=
A、1 B、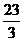 D、
D、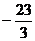
5.条件甲:“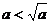 ”是条件乙:“
”是条件乙:“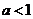 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.在首项为81,公差为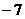 的等差数列
的等差数列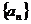 中,最接近零的项是
中,最接近零的项是
A.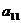 B.
B.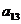 C.
C.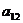 D.
D.
7.函数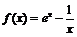 (其中
(其中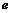 为自然对数的底数)的零点所在的区间是(
)
为自然对数的底数)的零点所在的区间是(
)
A.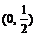 B.
B.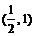 C.
C.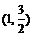 D.
D.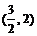
8.已知某个几何体的三视图如下,
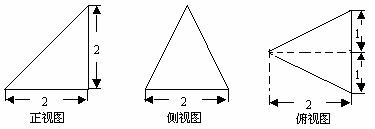
根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
A.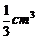 B.
B.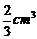 C.
C.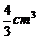 D.
D.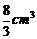
9.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积不小于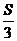 的概率是
的概率是
A.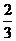 B.
B.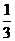 C.
C.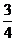 D.
D.
10.若不等式组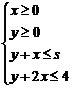 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则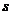 的取值范围是
的取值范围是
A.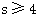 B.
B.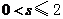 C.
C.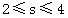 D.
D.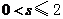 或
或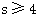
11. 统计某校1000名学生的数学会考成绩,得到样
本频率分布直方图如右图示,规定不低于60分为
及格,不低于80分为优秀,则及格人数是 ;
优秀率为 。
12.与直线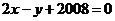 平行且与抛物线
平行且与抛物线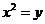 相切的直线方程是
。
相切的直线方程是
。
 13.甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是
13.甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是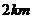 . 如图表示甲从家出发到乙同学家为止经过的路程
. 如图表示甲从家出发到乙同学家为止经过的路程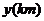 与时间
与时间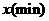 的关系, 其中甲在公园休息的时间是
的关系, 其中甲在公园休息的时间是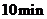 , 那么
, 那么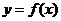 的表达式为 .
的表达式为 .
 14.(坐标系与参数方程选做题) 极坐标系中,曲线
14.(坐标系与参数方程选做题) 极坐标系中,曲线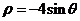 和
和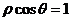 相交于点
相交于点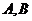 ,则
,则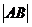 =
;
=
;
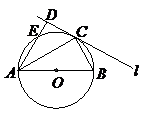
15.(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线 ,则点A到直线
,则点A到直线 的距离AD为 .
的距离AD为 .
16.(本题满分12分)已知向量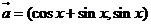 ,
,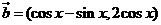 ,
,
设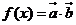 .
.
(1)求函数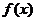 的最小正周期;
的最小正周期;
(2)当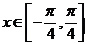 时,求函数
时,求函数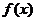 的最大值及最小值.
的最大值及最小值.
17. (本题满分12分)
已知函数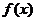 =
=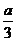 x3+bx2+4cx
x3+bx2+4cx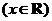 是奇函数,函数
是奇函数,函数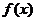 在点
在点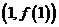 处的切线的斜率为-6, 且当x=2时,函数
处的切线的斜率为-6, 且当x=2时,函数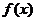 有极值.
有极值.
(I)求b的值;
(II)求函数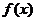 的解析式;
的解析式;
(Ⅲ)求函数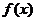 的单调区间.
的单调区间.
18. (本题满分14分) 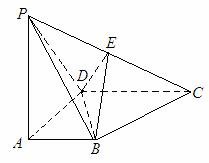 如图所示, 四棱锥P
如图所示, 四棱锥P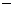 ABCD底面是直角梯形,
ABCD底面是直角梯形, 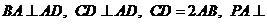 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明:
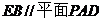 ;
;
(2)证明:
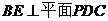 ;
;
(3)求三棱锥B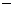 PDC的体积V.
PDC的体积V.
19. (本题满分14分)已知集合 ,在平面直角坐标系中,点
,在平面直角坐标系中,点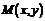 的坐标x∈A,y∈A。计算:
的坐标x∈A,y∈A。计算:
(1)点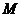 正好在第二象限的概率;
正好在第二象限的概率;
(2)点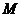 不在x轴上的概率;
不在x轴上的概率;
(3)点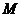 正好落在区域
正好落在区域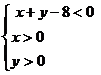 上的概率。
上的概率。
20. (本题满分12分) 已知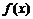 是定义在R上的函数,对于任意的实数a,b,都有
是定义在R上的函数,对于任意的实数a,b,都有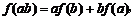
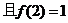 。
。
(Ⅰ)求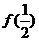 的值;
的值;
(Ⅱ)令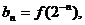 求证:
求证: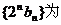 等差数列.
等差数列.
21. (本小题满分14分)
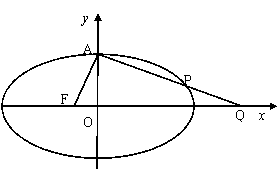 设椭圆C:
设椭圆C: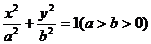 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且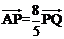 .
.
⑴求椭圆C的离心率;
⑵若过A、Q、F三点的圆恰好与直线l:
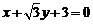 相切,求椭圆C的方程.
相切,求椭圆C的方程.
广东省梅县华侨中学2008届高考最后冲刺测试题
(文科数学)

