13、已知集合A={x∈R|ax2-3x+2=0,a∈R},若A中元素至多有1个,则a的取值范围是_________;
14、设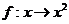 是集合A到集合B的映射,如果B={1,2},则
是集合A到集合B的映射,如果B={1,2},则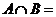 ;
;
15、有下列四个命题:(1)“若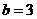 ,则
,则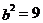 ”的逆命题;(2)“全等三角形的面积相等”的否命题;(3)“若
”的逆命题;(2)“全等三角形的面积相等”的否命题;(3)“若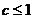 ,则
,则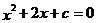 有实根”;(4)“若
有实根”;(4)“若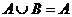 ,则
,则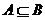 ”的逆否命题.其中真命题的个数是__________;
”的逆否命题.其中真命题的个数是__________;
16、若函数y=x3+ax2+bx+27在x=-1时有极大值,在x=3时有极小值,则a=___________,b=___________.
17、设函数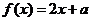 ,不等式
,不等式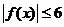 的解集是
的解集是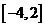 ,试求不等式
,试求不等式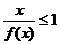 的解集.
的解集.
18、设有两个命题:
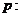 关于x的不等式x2+(a-1)x+a2>0的解集是R;
关于x的不等式x2+(a-1)x+a2>0的解集是R;
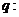 f (x)=
f (x)=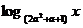 是减函数.且“p或q”为真命题, 求实数a的取值范围.
是减函数.且“p或q”为真命题, 求实数a的取值范围.
19、设f (x)=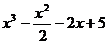
(1)求函数f(x)的单调递增、递减区间;
(2)当x∈[-1,2]时,f(x)<m恒成立,求实数m的取值范围.
20、已知向量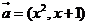
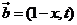 ,若函数
,若函数 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
21、已知 是函数
是函数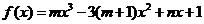 的一个极值点,其中
的一个极值点,其中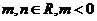 ,
,
(I)求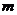 与
与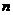 的关系式;
的关系式;
(II)求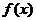 的单调区间;
的单调区间;
(III)当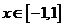 时,函数
时,函数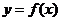 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3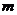 ,求
,求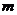 的取值范围.
的取值范围.
22、已知曲线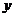 =
=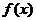 =
=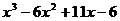 ,在它对应于
,在它对应于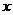
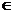 [0,2]的弧段上求一点P,使得曲线在该点的切线在
[0,2]的弧段上求一点P,使得曲线在该点的切线在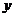 轴上的截距为最小,并求出这个最小值。
轴上的截距为最小,并求出这个最小值。
郑州四中2008―2009学年高三文科数学第一次调考答题卷
 一.选择题(本大题12小题,每小题5分,共60分)
一.选择题(本大题12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
13.________________; 14.____________ ; 15. _____________; 16. _______________.
 17.解:
17.解:
 18.解:
18.解:

 19.解:
19.解: 21.解:
21.解:
 郑州四中2008――2009学年高三文科数学第一次调考答案
郑州四中2008――2009学年高三文科数学第一次调考答案 ; 14.
; 14. 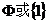 ; 15.1个; 16.
; 15.1个; 16. 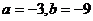 .
. 20.解:
20.解: