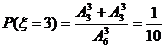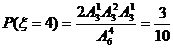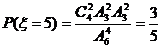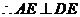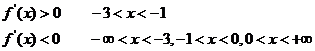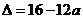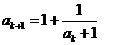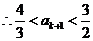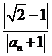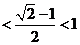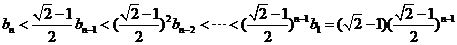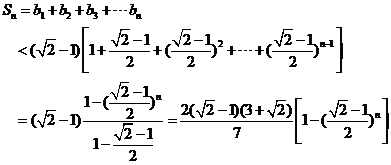1.设集合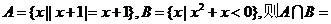
A.(-1,0)
B.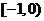 C.
C.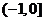 D.
D.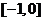
2.复数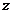 满足
满足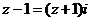 ,则
,则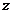 的值是
的值是
A.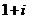 B.
B.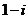 C.
C.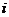 D.
D.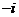
3.在某项测量中,测量结果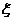 服从正态分布
服从正态分布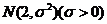 ,若
,若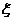 在(0,2)内取值的概率为0.4,则
在(0,2)内取值的概率为0.4,则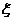 在
在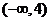 内取值的概率为
内取值的概率为
A.0.1 B.
4.双曲线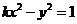 的一条渐进线与直线
的一条渐进线与直线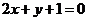 垂直,则此双曲线的离心率是
垂直,则此双曲线的离心率是
A.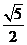 B.
B.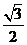 C.
C.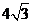 D.
D.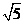
A.15,16,19 B.15,17,
6.点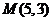 到抛物线
到抛物线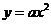 的准线的距离为6,那么抛物线的方程是
的准线的距离为6,那么抛物线的方程是
A.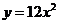 B.
B.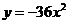
C.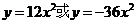 D.
D.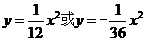
7.如果实数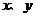 满足
满足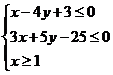 ,目标函数
,目标函数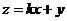 的最大值为12,最小值3,那么实数
的最大值为12,最小值3,那么实数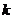 的值为
的值为
A.―2
B.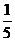 C.2
D.不存在
C.2
D.不存在
8.某教师一个上午有3个班级的课,每班一节,如果上午只能排四节课,并且教师不能连上三节课,那么这位师傅上午的课表的所有排法为
A.2
B.
9.设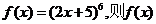 的导函数
的导函数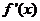 展开式中
展开式中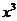 的系数为_________________。
的系数为_________________。
10.从装有 个球(其中
个球(其中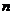 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出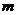 个球(
个球(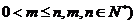
共有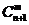 种取法,在这
种取法,在这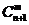 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的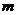 个球全部为白球;第二类是取出
个球全部为白球;第二类是取出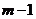 个白球,1个黑球,共有
个白球,1个黑球,共有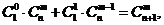 即有等式:
即有等式: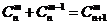 成立,试根据上述思想化简下列式子:
成立,试根据上述思想化简下列式子: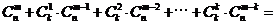 _______
_______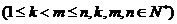
11.已知命题p: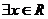 ,
,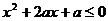 ,若命题
,若命题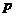 是假命题,则实数
是假命题,则实数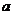 的取值范围是 .
的取值范围是 .
12.已知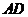 是
是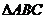 的中线,
的中线,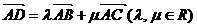 ,那么
,那么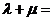 ;若
;若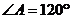 ,
,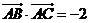 ,则
,则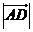 的最小值是
.
的最小值是
.
 13.(坐标系与参数方程选做题)在直角坐标系中,曲线
13.(坐标系与参数方程选做题)在直角坐标系中,曲线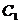 的参数方程为
的参数方程为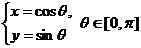 ,以
,以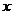 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线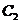 在极坐标系中的方程为
在极坐标系中的方程为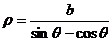 .若曲线
.若曲线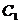 与
与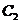 有两个不同的交点,则实数
有两个不同的交点,则实数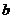 的取值范围是
.
的取值范围是
.
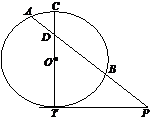
14.(几何证明选讲选做题)如图,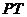 切⊙
切⊙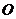 于点
于点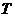 ,
,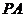 交⊙
交⊙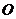 于
于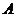 、
、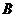 两点,且与直径
两点,且与直径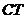 交于点
交于点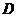 ,
,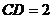 ,
,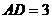 ,
,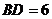 ,则
,则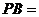 .
.
15.(不等式选讲选做题)若不等式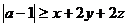 ,对满足
,对满足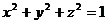 的一切实数
的一切实数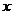 、
、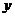 、
、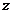 恒成立,则实数a的取值范围是
.
恒成立,则实数a的取值范围是
.
16.(本题满分12分) 在等腰△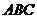 中,
中, 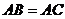 ,且
,且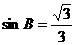 .
.
(Ⅰ)求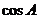 的值;
的值;
(Ⅱ)若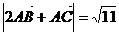 ,求
,求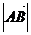 .
.
17.(本题满分12分)
某工厂由于工作失误,未贴标签前,把3箱含“三聚氰胺”的问题牛奶与合格的3箱牛
奶混到了一起,对这6箱牛奶逐箱进行检测,到确定出3箱问题奶粉为止,把3箱含“三
聚氰胺”的牛奶全部筛选出来需要的次数为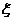
(1)求随即变量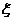 的分布列;
的分布列;
(2)求随即变量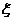 的期望
的期望
 18.(本题满分14分)
18.(本题满分14分)
如图,长方体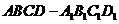 中,
中,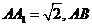
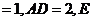 为
为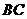 的中点
的中点
(1)求点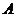 到面
到面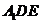 的距离;
的距离;
(2)设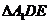 的重心为
的重心为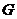 ,问是否存在实数
,问是否存在实数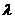 ,使
,使
得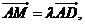 且
且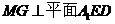 同时成立?若存
同时成立?若存
在,求出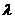 的值;若不存在,说明理由。
的值;若不存在,说明理由。
19.(本题满分14分)
函数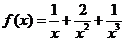 ;
;
(1)求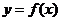 在
在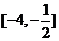 上的最值;
上的最值;
(2)若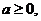 求
求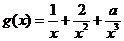 的极值点
的极值点
20(本题满分14分)如图, 已知定圆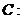
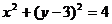 ,定直线
,定直线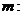
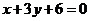 ,过
,过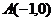 的一条动直线
的一条动直线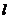 与直线相交于
与直线相交于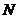 ,与圆
,与圆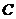 相交于
相交于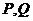 两点,
两点,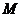 是
是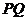 中点.
中点.
 (Ⅰ)已知
(Ⅰ)已知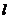 过圆心
过圆心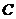 ,求证:
,求证: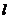 与
与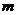 垂直;
垂直;
(Ⅱ)当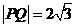 时,求直线
时,求直线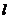 的方程;
的方程;
(Ⅲ)设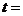
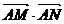 ,试问
,试问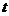 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出 的值;
的值;
若不为定值,请说明理由.
21.(本题满分14分)
数列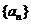 满足:
满足: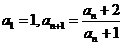
(I)求证: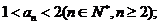
(Ⅱ)令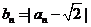
(1)求证: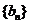 是递减数列;
是递减数列;
(2)设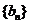 的前
的前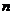 项和为
项和为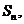 求证:
求证: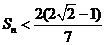
2009届盛兴中学高三模拟试卷数学(理科)
9.24000 10.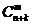 11.
11. 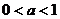 .
12.
.
12. 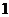 ;
;
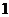 .
.
13.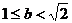 .
14.
.
14.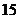 .
15.
.
15.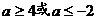 .
.
16解:(Ⅰ)在△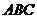 中,由
中,由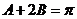 得
得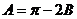 .
.
所以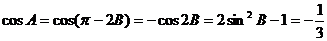 . …5分
. …5分
(Ⅱ)
由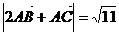 得
得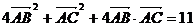 . ………………………….9分
. ………………………….9分
又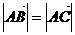 ,
,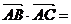
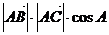 =
=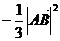 ; ………11分
; ………11分
于是有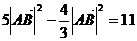 ,解得
,解得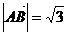
17、解:(1)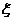 可能取的值为3,4,5
2分
可能取的值为3,4,5
2分
1.
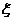
2. 3
3. 4
4. 5
5.
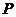
6.
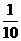
7.
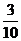
8.
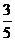
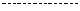 8分
8分
(2) 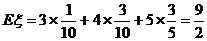
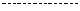 12分
12分
18. 解(1) 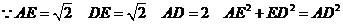
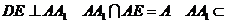 面
面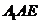
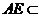 面
面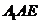
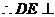 面
面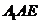
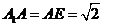
取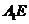 的中点H
的中点H 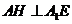
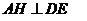
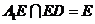
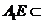 面
面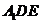
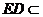 面
面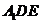
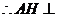 面
面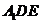
AH为点A到面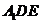 的距离
的距离
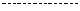 3分
3分
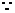 AH=1
AH=1 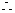 点A到面
点A到面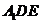 的距离为1
的距离为1 
 6分
6分
(2) 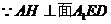 ,过点
,过点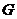 作
作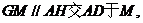
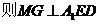 ,且
,且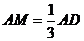
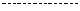 10分
10分
故存在实数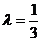 ,使得
,使得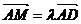 ,且
,且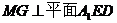 同时成立.
同时成立.
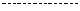 14分
14分
19.解:(1) 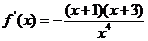
 1分
1分
9. x
10. -4
11. 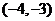
12. -3
13. (-3,-1)
14. -1
15. (-1,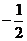 )
)
16. 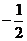
17. 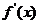
18.
19. -
20. 0
21. +
22. 0
23. -
24.
25. 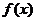
26. 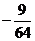
27. 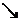
28. 极小值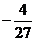
29. 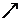
30. 极大值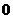
31. 
32. -2
 6分
6分
 最大值为0,最小值-2
最大值为0,最小值-2
 7分
7分
(2)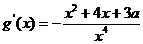
设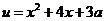
当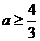 时,
时,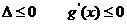 所以
所以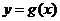 没有极值点
没有极值点 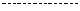 9分
9分
当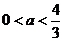 时,
时,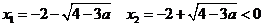
减区间: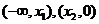 增区间:
增区间: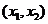
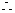 有两个极值点
有两个极值点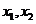
 11分
11分
当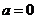 时,
时,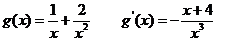
减区间: 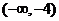 增区间:
增区间: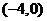
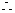 有一个极值点
有一个极值点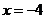
综上所述: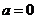 时
时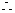 有一个极值点
有一个极值点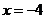 ;
;
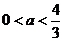 时有两个极值点
时有两个极值点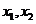 ;
;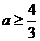 时没有极值点
时没有极值点 
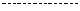 14分
14分
20.(本小题满分14分)
解: (Ⅰ) 由已知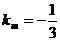 , 又圆心
, 又圆心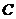
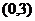 ,则
,则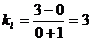 .故
.故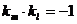 .
.
所以直线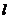 与
与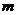 垂直.
………………………3分
垂直.
………………………3分
(Ⅱ) 当直线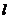 与
与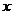 轴垂直时,易知
轴垂直时,易知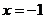 符合题意; ………………4分
符合题意; ………………4分
当直线与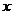 轴不垂直时,设直线
轴不垂直时,设直线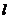 的方程为
的方程为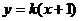 . …………5分
. …………5分
由于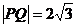 ,所以
,所以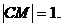
由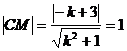 ,解得
,解得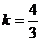 . ………………7分
. ………………7分
故直线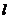 的方程为
的方程为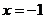 或
或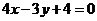 .
………………8分
.
………………8分
(Ⅲ)当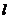 与
与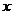 轴垂直时,易得
轴垂直时,易得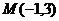 ,
,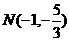 ,又
,又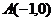 则
则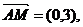
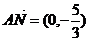 ,故
,故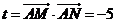 .
………………10分
.
………………10分
当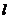 的斜率存在时,设直线
的斜率存在时,设直线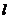 的方程为
的方程为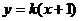 ,代入圆的方程得
,代入圆的方程得
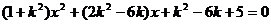 .则
.则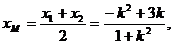
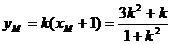 ,即
,即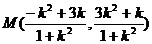 ,
,
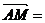
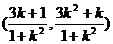 .又由
.又由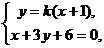 得
得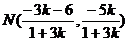 ,
,
则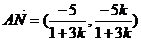 .
.
故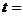
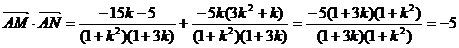 .
.
综上,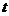 的值与直线
的值与直线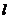 的斜率无关,且
的斜率无关,且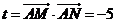 . …………14分
. …………14分
另解一:连结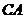 ,延长交
,延长交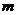 于点
于点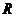 ,由(Ⅰ)知
,由(Ⅰ)知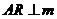 .又
.又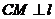 于
于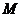 ,
,
故△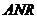 ∽△
∽△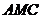 .于是有
.于是有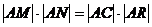 .
.
由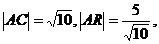 得
得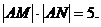
故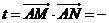
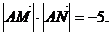 ………………………14分
………………………14分
21.解:(Ⅰ)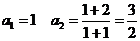
(1)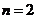 时
时 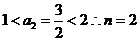 时不等式成立
时不等式成立 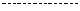 1分
1分
(2)假设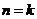 时不等式成立,即
时不等式成立,即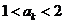
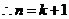 时不等式成立
时不等式成立
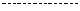 3分
3分
由(1)(2)可知对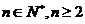 都有
都有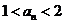
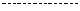 4分
4分
(Ⅱ)(1)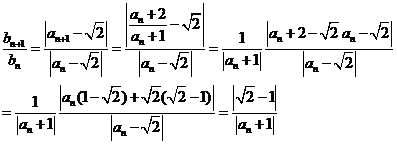
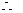
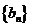 是递减数列
是递减数列
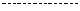 8分
8分
(2)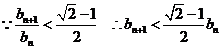
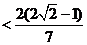
 14分
14分