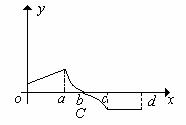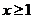1. 已知复数z满足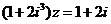 ,则z=( )
,则z=( )
A. 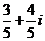 B. -
B. -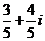 C. -
C. -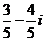 D.
D. 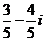
2. 集合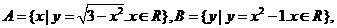 则
则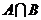 =( )
=( )
A. 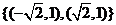 B.
B.
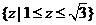
C. 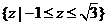 D.
D.
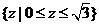
3. 在曲线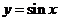 和
和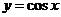 的交点
的交点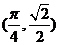 处,两切线的夹角为( )
处,两切线的夹角为( )
A. 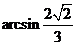 B.
B. 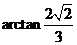 C.
C. 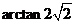 D.
D. 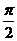
4. 已知点A(-3,-4),B(6,3)到直线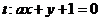 的距离相等,则实数
的距离相等,则实数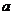 的值等于( )
的值等于( )
A. 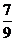 B. -
B. -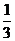 C. -
C. -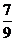 或-
或-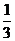 D.
D. 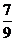 或
或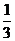
5. 不等式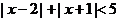 的解集为( )
的解集为( )
A. 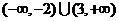 B.
B. 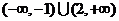 C. (-2,4) D. (-2,3)
C. (-2,4) D. (-2,3)
6. 在等差数列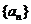 中,
中,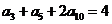 ,则此数列的前13项的和等于( )
,则此数列的前13项的和等于( )
A. 13 B.
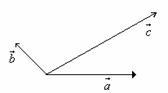 7. 如图,平面内向量
7. 如图,平面内向量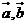 的夹角为1200,
的夹角为1200,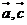 .的夹角为300,且
.的夹角为300,且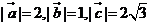 ,
,
若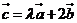 ,则
,则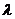 等于( )
等于( )
A. 1 B. -
8. 已知函数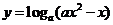 在区间[2,4]上是增函数,则实数
在区间[2,4]上是增函数,则实数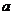 的取值范围是( )
的取值范围是( )
A. 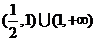 B.
B. 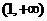 C. (
C. (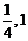 ) D. (0,
) D. (0,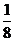 )
)
9. 某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一个镇去4名,另两镇各一名的概率为( )
A. 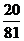 B.
B. 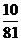 C.
C. 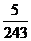 D.
D. 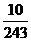
10. 在三棱锥A-BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为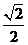 、
、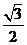 、
、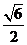 ,则三棱锥A-BCD的外接球的体积为( )
,则三棱锥A-BCD的外接球的体积为( )
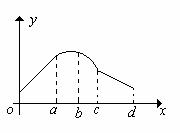 A.
A. 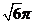 B.
2
B.
2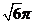 C.3
C.3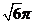 D. 4
D. 4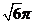
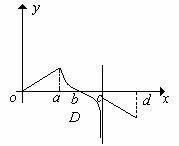
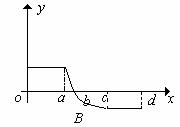
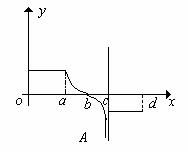
11. 已知函数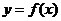 的图象如右图所示,
的图象如右图所示,
则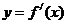 的大致图象可以是( )
的大致图象可以是( )
12. 双曲线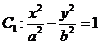 的左准线为
的左准线为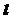 ,左焦点和右焦点分别为F1、F2,抛物线C2的准线为
,左焦点和右焦点分别为F1、F2,抛物线C2的准线为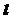 ,焦点为F2,C1与C2的一个交点为P,线段PF2的中点为M,O是坐标原点,则
,焦点为F2,C1与C2的一个交点为P,线段PF2的中点为M,O是坐标原点,则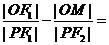 ( )
( )
A. -1 B. 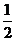 D.
D. 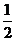
第Ⅱ卷(非选择题,共90分)
13. 若对于任意的实数x,都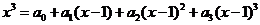 ,则实数
,则实数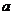 的值为
.
的值为
.
14. 三棱锥P-ABC中,PA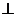 平面ABC,
平面ABC,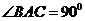 ,AB=AC=AP=2,D为AB中点,E为BC中点,则点D到直线PE的距离等于
.
,AB=AC=AP=2,D为AB中点,E为BC中点,则点D到直线PE的距离等于
.
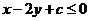 15. 已知
15. 已知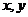 满足
满足 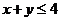 且目标函数
且目标函数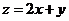 的最大值为7,则最小值
的最大值为7,则最小值
为 .
 16. 函数
16. 函数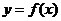 的图象是圆心在原点的
的图象是圆心在原点的
单位圆的两段弧(如图),则不等式
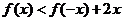 的解集为
.
的解集为
.
17. (本题满分10分)△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,向量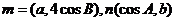 满足m∥n.
满足m∥n.
(1)求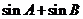 的取值范围;
的取值范围;
(2)若实数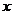 满足
满足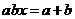 ,试确定
,试确定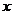 的取值范围.
的取值范围.
18. (本题满分12分)3名志愿者在
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记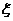 表示这3名志愿者在
表示这3名志愿者在 的分布列.
的分布列.
 19. (本题满分12分)如图,ABCD
19. (本题满分12分)如图,ABCD
是边长为
且二面角C-AB-F是直二面角,
AF=a,G是EF的中点.
(1)求证:平面AGC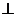 平面BGC;
平面BGC;
(2)求GB与平面AGC所成角的大小;
(3)求二面角B-AC-G的大小.
20. (本题满分12分)设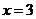 是函数
是函数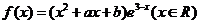 的一个极值点。
的一个极值点。
(1)求a与b的关系式(用a表示b),并求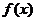 的单调区间;
的单调区间;
(2)设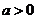 ,
,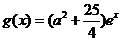 ,若存在
,若存在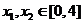 使得
使得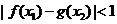 成立,求a的取值范围.
成立,求a的取值范围.
21. (本题满分12分)已知A、B两点在抛物线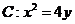 上,点
上,点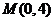 满足
满足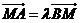 .
.
(Ⅰ)求证: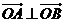 ;
;
(Ⅱ)设抛物线C过A、B两点的切线交于点N;
(1)求证:点N在一条定直线上;
(2)设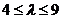 ,求直线MN在x轴上截距的取值范围.
,求直线MN在x轴上截距的取值范围.
22. (本题满分12分)数列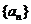 满足:
满足: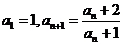 .
.
(Ⅰ)求证: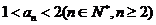 ;
;
(Ⅱ)令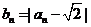 ;
;
(1)求证: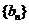 是递减数列;
是递减数列;
(2)设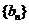 的前n项和为
的前n项和为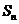 ,求证:
,求证: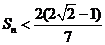 .
.