1.
复数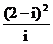 (i是虚数单位)在复平面上对应的点位于( )
(i是虚数单位)在复平面上对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合M={-1, 0, 1},N={x|x=ab, a, b∈M且a≠b},则集合M与集合N的关系是()

 A. M=N B.
M
A. M=N B.
M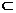 N C.
M
N C.
M 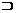 N D.
M
N D.
M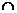 N=
N=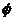
 3.命题p:不等式|x|+|x+1|>a的解集为R,命题q:f(x)=-(7
3.命题p:不等式|x|+|x+1|>a的解集为R,命题q:f(x)=-(7
A. (1, 2) B. [1, 2) C. (-∞, 1) D. (-∞, 2)
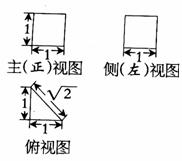
4. 已知某几何体的三视图如右图所示,它的表面积是( )
A. 4+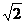 B.
2+
B.
2+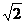
C. 3+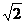 D.
6
D.
6
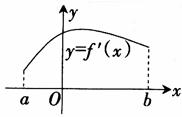 5. 已知f5′(x)是函数f (x)的函导数,在区间[a, b]上f ′(x)的图象如右图所示,如果f (a) f
(b)<0,则函数f (x)在区间(a, b)上( )
5. 已知f5′(x)是函数f (x)的函导数,在区间[a, b]上f ′(x)的图象如右图所示,如果f (a) f
(b)<0,则函数f (x)在区间(a, b)上( )
A. 至少有一个零点 B. 至多有一个零点
C. 没有零点 D. 必有唯一的零点
 6.设α,β,γ是三个不重合的平面,m, n是两条不重合的直线,给出下列命题:①若α⊥β,β⊥γ,则α⊥γ;②若m∥α, n∥β, α⊥β,则m⊥n;③若α∥β,γ∥β,则α∥γ;④若α∥β且m与α,n与β所成的角相等,则m∥n。其中错误命题的个数为( )
6.设α,β,γ是三个不重合的平面,m, n是两条不重合的直线,给出下列命题:①若α⊥β,β⊥γ,则α⊥γ;②若m∥α, n∥β, α⊥β,则m⊥n;③若α∥β,γ∥β,则α∥γ;④若α∥β且m与α,n与β所成的角相等,则m∥n。其中错误命题的个数为( )
A. 0 B.
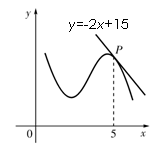
7.函数y=f(x)的图象在点P处的切线方程是y=-2x+15,如图,
则f(5)+ f ′(5)=( )
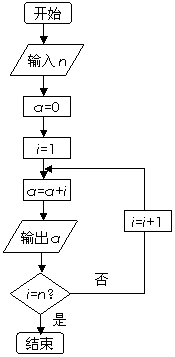 A.1
B.
2 C.
3 D.
4
A.1
B.
2 C.
3 D.
4
8. 若数列{an}的前n项由如图所示的程序框图中输出
的a的值依次给出,则数列{an}的通项公式an=( )
A. 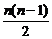 B.
n C.
n-1 D.
B.
n C.
n-1 D.
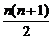
9. 抛物线y=ax2的焦点恰好为双曲线y2-x2=2的上焦点,则a=( )
 A.
A.
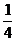 B.
B.
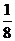 C.
C.
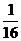 D.
1
D.
1
10. 若a1=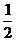 , a2=
, a2=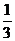 , an・an+2=1(n∈N*),则a2008+a2009等于( )
, an・an+2=1(n∈N*),则a2008+a2009等于( )
A. 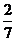 B.
B.
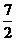 C.7 D. 2
C.7 D. 2
11. 已知f (x)为偶函数,且f (2+x)=f (2-x),当-2≤x≤0时,f (x)=2x, an=f (n), n∈N*,则a2009=( )
A. 2009 B. 2 C.
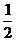 D.
-2
D.
-2
12. 在区间[1,4]内取数a,在区别[0,3]内取数b,使函数f (x)=ax2+2x+b有两个相异零点的概率是( )
A. 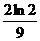 B.
B.
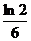 C.
C.
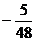 D.
D.
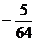
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷包括填空题和解答题共两个大题.
2.第Ⅱ卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置上.
13.在(x4+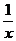 )10的展开式中,常数项是 (用具体数字作答)
)10的展开式中,常数项是 (用具体数字作答)
 14.某人练习打靶,一共打了8枪,中了3枪,其中恰有2发连中,则中靶方一共有 种。
14.某人练习打靶,一共打了8枪,中了3枪,其中恰有2发连中,则中靶方一共有 种。
15.
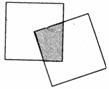
现有一个关于平面图形的命题:如图,同一平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积为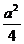 . 类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
. 类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
16.
定义一种运算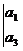
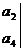 =a1a4-a2a3.
将函数f
(x)=
=a1a4-a2a3.
将函数f
(x)= 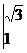
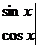 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为 .
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为 .
17.(本小题满分12分)
已知点A (2,0), B (0,2),
C (cos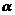 , sin
, sin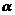 ).
).
(1)若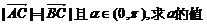 ;
;
(2)若f (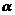 )=
)= 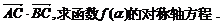
18.(本小题满分12分)
在一次抗洪抢险中,准备用射击的方法引爆从上游漂流而下的一巨大汽油罐。已知只有5发子弹,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中概率都是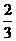 ,且每次命中与否互相独立.
,且每次命中与否互相独立.
(1)求油罐被引爆的概率;
(2)如果油罐引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。
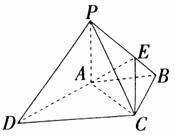
如图,四棱锥P―ABCD中,PA⊥底面ABCD,PC⊥AD。底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求平面AEC和平面PBC所成锐二面角的余弦值。
20.(本小题满分12分)
已知数列{an}满足an+1=2an+n+1(n=1,2,3,……).
(1)若a1=-1,求证数列{an+n+2}为等比数列,并求{an}的前n项和Sn.
(2)求证{an}不可能是等比数列;
21.(本小题满分12分)
已知椭圆C的中心在原点,焦点在x轴上,点F1、F2分别是椭圆的左、右焦点,在直线x=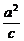 (a、c分别为椭圆的长半轴和半焦距的长)上的点P(2,
(a、c分别为椭圆的长半轴和半焦距的长)上的点P(2, 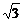 ),满足线段PF1的中垂线过点F2,直线l:y=kx+m为动直线,且直线l与椭圆C交于不同的两点A、B.
),满足线段PF1的中垂线过点F2,直线l:y=kx+m为动直线,且直线l与椭圆C交于不同的两点A、B.
(1)求椭圆C的方程;
(2)若在椭圆C上存在点Q,满足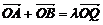 (O为坐标原点),求实数λ的取值范围.
(O为坐标原点),求实数λ的取值范围.
22.(本小题满分14分)
设函数f(x)=(1+x)2-ln(1+x)2.
(1)求函数f(x)的单调区间;
(2)当x∈[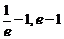 ]时,不等式f (x)<m恒成立,求实数m的取值范围;
]时,不等式f (x)<m恒成立,求实数m的取值范围;
(3)已知g(x)=x2+x+a,若函数f(x)的图象与函数g(x)的图象在0≤x≤2时恰有两个相异的交点,求实数a的取值范围.
寿光市2009年高考适应性训练试题