1.已知等差数列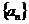 的首项为1,公差为2,则a8的值等于( )
的首项为1,公差为2,则a8的值等于( )
A.13
B.
2.函数y= +
+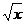 的定义域为( )
的定义域为( )
A. B.
B.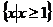 C.
C.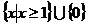 D.
D.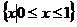
3.若a<0,0<b<1,那么( )
A.a>ab>ab2 B.ab2>ab>a C.ab>a>ab2 D.ab>ab2>a
4.一元二次不等式ax2+bx+2>0的解集是(-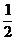 ,
, ),则a+b的值是( )
),则a+b的值是( )
A.10
B.
5.已知等差数列 中,前n项和为Sn,若a3+a9=6,则S11=( )
中,前n项和为Sn,若a3+a9=6,则S11=( )
A.12
B.
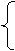
x-y+1≥0
y+1≥0
x+y-1≤0
6.若实数x、y满足条件
A.-3
B.
7.下列结论正确的是( )
A.当x>0且x≠1时,lgx +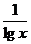 ≥2
B.当x>0时,
≥2
B.当x>0时,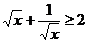
C.当x≥2时,x+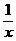 的最小值为2
D.当0<x≤2时,x -
的最小值为2
D.当0<x≤2时,x -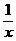 无最大值
无最大值
8.在△ABC中,若tanA・tanB>1,那么△ABC是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰三角形

 9.用单位立方体搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最小值与最大值分别为( )
9.用单位立方体搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最小值与最大值分别为( )
A.9,13 B.7,10
C.10,16 D.10,15
正视图 俯视图
10.把正偶数列{2n}的各项从小到大依次排成如图所示的 2
三角形状数表,设M(r,t)表示表中第r行的第t个数,则表 4 6
中的数2008对应于( ) 8 10 12
A.M(45,14) B.M(45,24) 14 16 18 20
C.M(46,14) D.M(46,15) … … … … …
11.在△ABC中,已知a=7,b=3,c=5,则该三角形的最大内角度数是 。
12.等比数列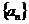 中,a4=
中,a4=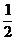 ,a8=8,则a
,a8=8,则a
13.已知点(2,1)和(-3,2)在直线2x-y+a=0的两侧,则a的取值范围是 。
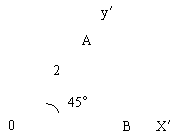
 14.如右图所示的直观图,
14.如右图所示的直观图,
其原来平面图形的面积是 。
15.x、y
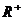 ,且
,且 =1,
=1,
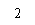 则x+y的最小值为
。
则x+y的最小值为
。
16.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上。继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船是每小时航行 海里。
17.定义一种运算“*”,它对于正整数满足下列运算性质;
①2*2006=1;
②(2n+2)* 2006=3[(2n)*2006];
则2008*2006的值是 。
第Ⅱ卷
18.已知全集U=R,A=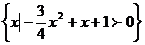 ,B=
,B= ,求Cu(A
,求Cu(A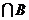 )。
)。
19.已知等比数列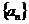 ,
, 
(1)求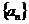 的通项公式;
的通项公式;
(2)令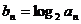 ,求数列
,求数列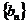 的前n项和
的前n项和
20.某单位用2160万元购得一块空地,计划在该地块建造一栋至少10层,每层2000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x
(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
21.在△ABC中,内角A、B、C对边的长分别是a、b、c,已知c=2,C= 。
。
(1)若△ABC的面积等于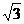 ,求a、b;
,求a、b;
(2)若sinB=2sinA,求△ABC的面积。
22.设数列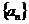 的前n项和Sn=n2-4n+4。
的前n项和Sn=n2-4n+4。
(1)求数列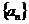 的通项公式;
的通项公式;
(2)求和Tn= ;
;
(3)设各项均不为0的数列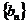 中,所有满足bi・bi+1<0的整数i的个数称为这个数列
中,所有满足bi・bi+1<0的整数i的个数称为这个数列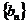 的变号数,令bn=1-
的变号数,令bn=1-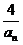 (n
(n N*),求数列
N*),求数列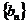 的变号
的变号
 杭绍金温衢七校2008学年第二学期期中联考答题卷
杭绍金温衢七校2008学年第二学期期中联考答题卷
高一数学
命 题:张水华 审核:刘春华
考试时间:120分钟 总分:150分
题号
1
2
3
4
5
6
7
8
9
10
答案
11、 12、
13、 14、
15、 16、
17、
(本大题共5个小题,第18至20题,每题各14分,第21、22题15分)
18、
19、
20、
21、
22、
杭绍金温衢七校2008学年第二学期期中联考卷


