1.不等式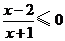 的解集是________.
的解集是________.
2. 已知: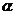 为第四象限角,且
为第四象限角,且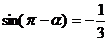 ,则
,则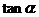 =________.
=________.
3. 已知:A=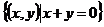 ,B=
,B=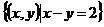 ,则A∩B=_________.
,则A∩B=_________.
4. 直线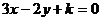 在两坐标轴上的截距之和为2,则实数
在两坐标轴上的截距之和为2,则实数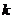 的值是_____.
的值是_____.
5. 在等比数列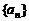 中,
中,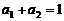 ,
,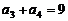 ,则
,则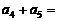 ________.
________.
6. 对于函数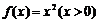 图象上任意两点
图象上任意两点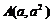 ,
,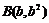 ,直线段AB必在曲线段AB的上方,则由图象的特征可得不等式
,直线段AB必在曲线段AB的上方,则由图象的特征可得不等式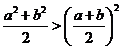 .请分析
.请分析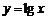 的图象特征,类比上述不等式可以得到 .
的图象特征,类比上述不等式可以得到 .
7. 若AD为△ABC的角平分线,满足AD=AB=2,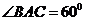 ,则CD=_________.
,则CD=_________.
8. 已知平面上不同的四点A、B、C、D,若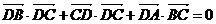 ,
,
则△ABC是_________三角形.
9. 某医疗研究所为了检验某种血清预防感冒的作用,把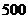 名使用血清的人与另外
名使用血清的人与另外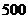 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设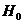 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用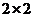 列联表计算得
列联表计算得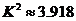 ,经查对临界值表知
,经查对临界值表知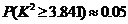 .
.
对此,四名同学做出了以下的判断:
p:有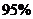 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
q:若某人未使用该血清,那么他在一年中有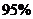 的可能性得感冒
的可能性得感冒
r:这种血清预防感冒的有效率为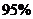
s:这种血清预防感冒的有效率为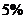
则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上)
(1) p∧?q ; (2)?p∧q ;
(3)(?p∧?q)∧(r∨s); (4)(p∨?r)∧(?q∨s)
10. 椭圆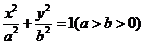 的左右焦点分别为F1 ?F2,在椭圆上存在点P,满足
的左右焦点分别为F1 ?F2,在椭圆上存在点P,满足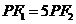 。则此椭圆的离心率e的取值范围是
.
。则此椭圆的离心率e的取值范围是
.
11. 设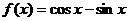 ,把
,把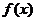 的图象向右单位平移m(m>0)个单位后,图象恰好为函数
的图象向右单位平移m(m>0)个单位后,图象恰好为函数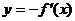 的图象,则m的最小值为________.
的图象,则m的最小值为________.
12. 已知函数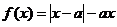 存在最小值,则实数
存在最小值,则实数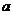 的取值范围是
.
的取值范围是
.
13. 设x,y均为正实数,且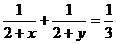 ,则xy的最小值为________.
,则xy的最小值为________.
14. 已知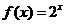 可以表示成一个奇函数
可以表示成一个奇函数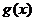 与一个偶函数
与一个偶函数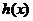 之和,若关于
之和,若关于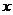 的不等式
的不等式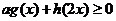 对于
对于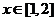 恒成立,则实数
恒成立,则实数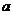 的最小值是
.
的最小值是
.
15. A袋中有1张10元和1张5元的钱币,B袋中有2张10元和1张5元的钱币,从A袋中任取一张钱币与B袋任取一张钱币互换,这样的互换进行了一次后:
求(1)A袋中10元钱币恰是一张的概率;
(2)A袋中10元钱币至少是一张的概率.
 16. 已知四棱锥P-ABCD,底面ABCD是
16. 已知四棱锥P-ABCD,底面ABCD是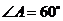 、边长为
、边长为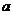 的菱形,又
的菱形,又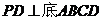 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN//平面PMB;
(2)证明:平面PMB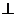 平面PAD;
平面PAD;
(3)求点A到平面PMB的距离.
17. 已知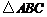 的面积为
的面积为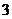 ,且满足
,且满足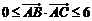 ,设
,设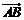 和
和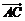 的夹角为
的夹角为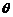 .
.
(1)求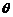 的取值范围;
的取值范围;
(2)求函数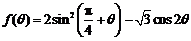 的最大值与最小值.
的最大值与最小值.
18. 已知直线l1:x+my-m-2=0与x轴交于点A,直线l2:mx-y
(1)求证:A,M,B,O四点共圆,并写出圆的方程;
(2)当AB与OM垂直于点P时,求证:点P与四边形AMBO其中一边中点的连线与对边垂直.
19. 设n为给定的正整数,记An={x|2n<x<2n+1,且x=
(1)当n为奇数时,求An中的最大数和最小数;
(2)求An中所有元素之和.
20. 已知二次函数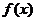 的二次项系数为
的二次项系数为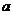 ,且不等式
,且不等式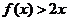 的解集为
的解集为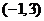 .
.
(1)若函数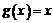
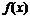 在区间
在区间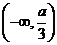 内单调递减,求
内单调递减,求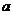 的取值范围;
的取值范围;
(2)当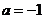 时,证明方程
时,证明方程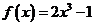 仅有一个实数根.
仅有一个实数根.
(3)当x∈[0,1]时,试讨论|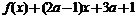 |≤3成立的充要条件.
|≤3成立的充要条件.
命题、校对:唐一良、张福俭
江苏省扬州中学2009届高三5月模拟考试
附加题
选修4-1――4-4(其中1、2、3、4题任选2题解答;5、6为必做题)
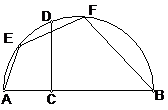 1.如图,AB为半圆直径,D为AB上一点,分别在半圆上取点E、F,使EA=DA,FB=DB.过D作AB的垂线,交半圆于C.求证:CD平分EF.
1.如图,AB为半圆直径,D为AB上一点,分别在半圆上取点E、F,使EA=DA,FB=DB.过D作AB的垂线,交半圆于C.求证:CD平分EF.
2.自然界生物种群的成长受到多种条件因素的影响,比如出生率、死亡率、资源的可利用性与竞争、捕食者的猎杀乃至自然灾害等等.因此,它们和周边环境是一种既相生又相克的生存关系.但是,如果没有任何限制,种群也会泛滥成灾.现假设两个互相影响的种群X,Y随时间段变化的数量分别为{an},{bn},并有关系式,其中a1=1,b1=1,试分析20个时段后这两个种群的数量变化趋势.
3.过抛物线y2=2px(p>0)的焦点F任作一弦AB=4p,建立适当的极坐标系,求OA的极角.(O为极点)
4.已知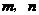 为正整数,用数学归纳法证明:当
为正整数,用数学归纳法证明:当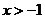 时,
时,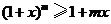 ;
;
5.抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列
(1)求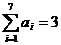 的概率; (2)若
的概率; (2)若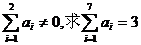 的概率.
的概率.
6. 2条直线将一个平面最多分成4部分,3条直线将一个平面最多分成7部分,4条直线将一个平面最多分成11部分,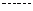 ;4=
;4=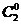
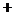
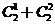 ,7=
,7=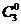
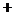
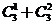 ,11=
,11=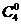
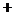
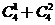 ;
;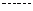 .
.
(1)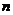 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(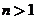 )?证明你的结论;
)?证明你的结论;
(2)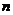 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分(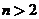 )?证明你的结论.
)?证明你的结论.
命题、校对:唐一良、张福俭
江苏省扬州中学2009届高三5月模拟考试

