1.若集合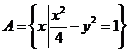 ,则
,则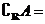 .
.
2.不等式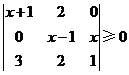 的解为
.
的解为
.
3.设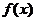 的反函数为
的反函数为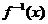 ,若函数
,若函数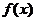 的图像过点
的图像过点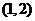 ,且
,且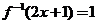 , 则
, 则
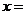 .
.
4.若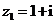 ,
,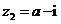 ,其中
,其中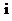 为虚数单位,且
为虚数单位,且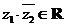 ,则实数
,则实数 .
.
 5.二项式
5.二项式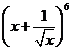 的展开式中的常数项为
.
的展开式中的常数项为
.
6.若点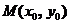 是圆
是圆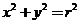 内异于圆心的点,则直线
内异于圆心的点,则直线
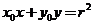 与该圆的位置关系是
.
与该圆的位置关系是
.
7.若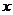 、
、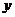 满足
满足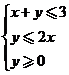 ,则
,则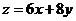 的最大值是 .
的最大值是 .
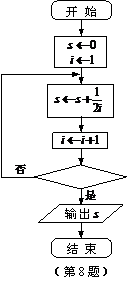
8.右图给出的是计算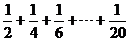 的值的一个框图,
的值的一个框图,
其中菱形判断框内应填入的条件是 .
9.在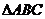 中,设角
中,设角 、
、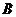 、
、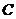 所对的边分别是
所对的边分别是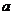 、
、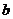 、
、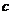 ,若
,若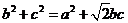 ,
,
且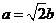 , 则
, 则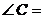 .
.
10.若函数 能使得不等式
能使得不等式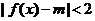 在区间
在区间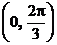 上恒成立,则实数
上恒成立,则实数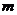 的取值范围是
.
的取值范围是
.
11.在平面直角坐标系中,若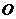 为坐标原点,则
为坐标原点,则 、
、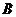 、
、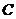 三点在同一直线上的充要条件为存在惟一的实数
三点在同一直线上的充要条件为存在惟一的实数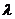 ,使得
,使得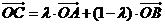 成立,此时称实数
成立,此时称实数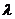 为“向量
为“向量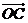 关于
关于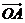 和
和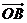 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知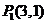 、
、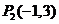 ,且向量
,且向量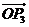 是直线
是直线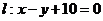 的法向量,则“向量
的法向量,则“向量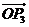 关于
关于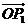 和
和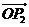 的终点共线分解系数”为
.
的终点共线分解系数”为
.
12.若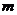 、
、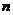 为两条不同的直线,
为两条不同的直线,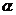 、
、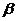 为两个不同的平面,则以下命题正确的是( )
为两个不同的平面,则以下命题正确的是( )
A.若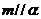 ,
,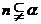 ,则
,则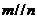 ; B.若
; B.若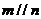 ,
,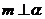 ,则
,则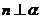 ;
;
C.若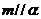 ,
,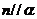 ,则
,则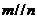 ; D.若
; D.若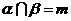 ,
,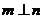 ,则
,则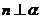 .
.
13.若函数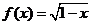 ,则当
,则当 时,
时,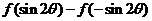 可化简为
可化简为
( )
A. ; B.
; B.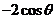 ; C.
; C.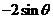 ; D.
; D.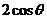 .
.
14.设数列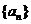 的前
的前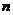 项之和为
项之和为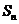 ,若
,若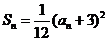 (
(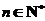 ),则
),则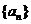 ( )
( )
A.是等差数列,但不是等比数列; B.是等比数列,但不是等差数列;
C.是等差数列,或是等比数列; D.可以既不是等比数列,也不是等差数列.
15.关于函数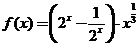 和实数
和实数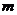 、
、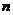 的下列结论中正确的是 ( )
的下列结论中正确的是 ( )
A.若 ,则
,则 ; B.若
; B.若 ,则
,则 ;
;
C.若 ,则
,则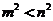 ; D.若
; D.若 ,则
,则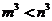 .
.
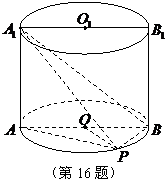 16. (本题满分12分,第1小题4分,第2小题8分)
16. (本题满分12分,第1小题4分,第2小题8分)
如图,已知点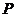 在圆柱
在圆柱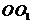 的底面圆
的底面圆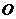 上,
上,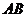
为圆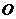 的直径.
的直径.
(1)求证: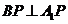 ;
;
(2)若圆柱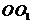 的体积
的体积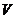 为
为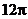 ,
, ,
,
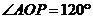 ,求异面直线
,求异面直线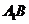 与
与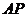 所成的角(用
所成的角(用
反三角函数值表示结果).
17. (本题满分14分,第1小题6分,第2小题8分)
袋中有8个仅颜色不同,其它都相同的球,其中1个为黑球,3个为白球,4个为红球.
(1)若从袋中一次摸出2个球,求所摸出的2个球恰为异色球的概率;
(2)若从袋中一次摸出3个球,求所摸得的3球中,黑球与白球的个数都没有超过红球的个数的不同摸法的种数.
18. (本题满分14分,第1小题6分,第2小题8分)
已知数列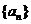 的前
的前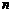 项和为
项和为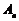 ,且对任意正整数
,且对任意正整数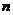 ,都满足:
,都满足: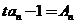 ,其中
,其中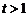 为实数.
为实数.
(1)求数列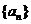 的通项公式;
的通项公式;
(2)若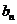 为杨辉三角第
为杨辉三角第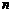 行中所有数的和,即
行中所有数的和,即 ,
, 为杨辉三角前
为杨辉三角前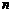 行中所有数的和,亦即为数列
行中所有数的和,亦即为数列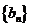 的前
的前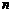 项和,求
项和,求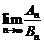 的值.
的值.
19.(本题满分17分,第1小题6分,第2小题11分)
已知函数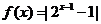 ,
,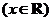 .
.
(1)证明:函数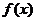 在区间
在区间 上为增函数,并指出函数
上为增函数,并指出函数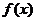 在区间
在区间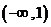 上的单调性;
上的单调性;
(2)若函数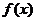 的图像与直线
的图像与直线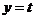 有两个不同的交点
有两个不同的交点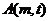 ,
,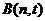 ,其中
,其中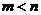 ,求
,求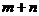 的取值范围.
的取值范围.
20. (本题满分18分,第1小题4分,第2小题5分,第3小题9分)
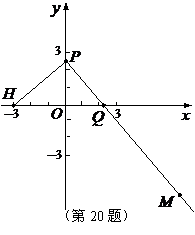 如图,已知点
如图,已知点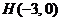 ,动点
,动点 在
在 轴上,点
轴上,点
在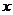 轴上,其横坐标不小于零,点
轴上,其横坐标不小于零,点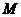 在直线
在直线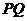 上,
上,
且满足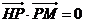 ,
,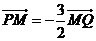 .
.
(1)当点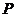 在
在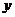 轴上移动时,求点
轴上移动时,求点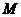 的轨迹
的轨迹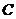 ;
;
(2)过定点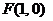 作互相垂直的直线
作互相垂直的直线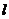 与
与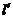 ,
,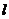 与
与
(1)中的轨迹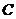 交于
交于 、
、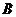 两点,
两点,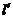 与(1)中的轨迹
与(1)中的轨迹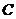 交于
交于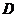 、
、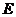 两点,求四边形
两点,求四边形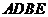 面积
面积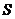 的最小值;
的最小值;
(3)将(1)中的曲线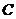 推广为椭圆:
推广为椭圆: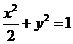 ,并将(2)中的定点取为焦点
,并将(2)中的定点取为焦点
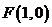 ,求与(2)相类似的问题的解.
,求与(2)相类似的问题的解.
上海市卢湾区2009年高考模拟考试

