1.设全集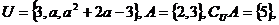 则a的值为
则a的值为
A.2或-4 B.2 C.-4 D.4
2.如果命题“若p则q”的逆命题是真命题,则下列命题一定为真命题的是
A.若p则q B.若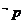 则
则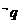 C.若
C.若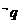 则
则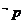 D.以上均不对
D.以上均不对
3.下面的说法正确的是:
A.所有单位向量相等 B.所有单位向量平行
C.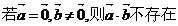 D.
D.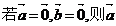 ∥
∥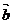
4.一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是
A.异面 B. 相交 C. 平行 D. 不确定
5.设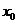 是方程
是方程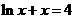 的解,则
的解,则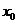 属于区间
属于区间
A. (0,1) B. (1,2) C. (2,3) D.(3,4)
6.函数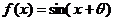 满足对任意
满足对任意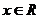 有
有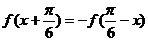 ,则
,则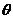 可以是:
可以是:
 A.
A.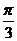 B.
B.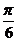
C.-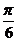 D.-
D.-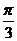
7.将一张坐标纸折叠一次,使得点M(0,4)与点N(1,3)重合,则与点P(2004,2010)重合的点的坐标是
A.(2006,2006) B.(2006,2007)
C.(2007,2006) D.(2007,2007)
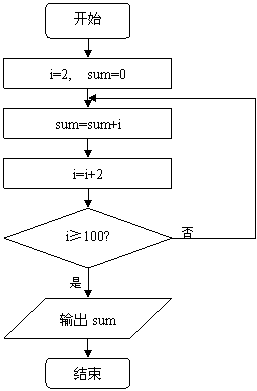
8.如右面的程序框图,那么,输出的数是
A.2450 B. 2550
C. 5050 D. 4900
9.等差数列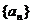 中,
中,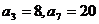 ,若数
,若数
列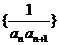 的前
的前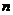 项和为
项和为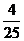 ,则
,则 的值为
的值为
A、14 B、15
C、16 D、18
10.定义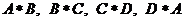 的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是
的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是

(1) (2) (3) (4) (A) (B)
A、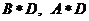 B、
B、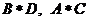 C、
C、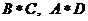 D、
D、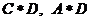
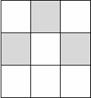 11.如图,一颗豆子随机扔到桌面上,假设豆子不落在线上,则它落在阴影区域的概率为________.
11.如图,一颗豆子随机扔到桌面上,假设豆子不落在线上,则它落在阴影区域的概率为________.
12.已知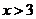 ,则函数
,则函数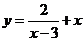 的最小值为
.
的最小值为
.
13.知a、b、c分别是△ABC中角A、B、C的对边,且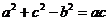 .则角
.则角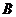 的大小是 .
的大小是 .
请从下面两题中选做一题,如果两题都做,以第一题的得分为最后得分.
 14.(坐标系与参数方程选做题)极坐标方程分别为
14.(坐标系与参数方程选做题)极坐标方程分别为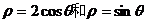 的两个圆的圆心距为
.
的两个圆的圆心距为
.
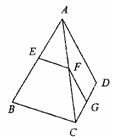
15.(几何证明选讲选做题)如图,在四边形ABCD中,EF//BC,FG//AD,则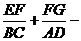 .
.
16.(本小题满分12分)
已知向量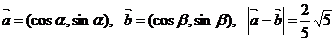 ,
,
(Ⅰ)求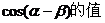 ;
;
(Ⅱ)若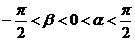 ,且
,且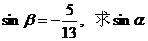 的值.
的值.
17.(本小题满分12分)
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
 18.(本小题满分14分)
18.(本小题满分14分)
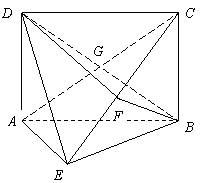
如图,矩形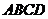 中,
中,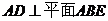 ,
,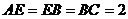 ,
,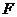 为
为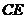 上的点,且
上的点,且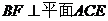 .
.
(Ⅰ)求证: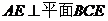 ;
;
(Ⅱ)求证;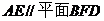 ;
;
(Ⅲ)求三棱锥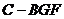 的体积.
的体积.
19.(本小题满分14分)
已知圆C: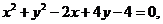 是否存在斜率为1的直线
是否存在斜率为1的直线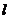 ,使
,使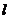 被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程,若不存在说明理由.
被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程,若不存在说明理由.
20.(本小题满分14分)
已知数列al,a2…,a30,其中al,a2…,a10是首项为1公差为1的等差数列;al0,a11…,a20是公差为d的等差数列;a20,a21…,a30是公差为d2的等差数列(d>0).
(Ⅰ)若a20=40,求 d;
(Ⅱ)试写出a30关于d的关系式,并求a30的取值范围;
(Ⅲ)请依次类推,续写己知数列,把已知数列推广为无穷数列.再提出同(2)类似的问题,并进行研究,你能得到什么样的结论?
21.(本小题满分14分)
已知函数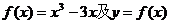 上一点P(1,-2),过点P作直线l,
上一点P(1,-2),过点P作直线l,
(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;
(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);
(Ⅲ)在(Ⅱ)的条件下,求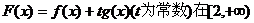 上单调时,t的取值范围.
上单调时,t的取值范围.
潮阳一中2007-2008学年度高三级摸底考试

