1. 已知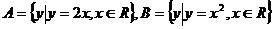 ,则
,则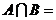
A.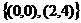 B.
B. C.
C.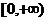 D.
D. 
2. 已知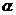 为第二象限的角,且
为第二象限的角,且 ,则
,则
A.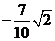 B.
B. C.
C.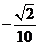 D.
D.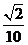
3. 设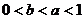 ,则下列不等式成立的是
,则下列不等式成立的是
 A.
A. 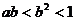 B.
B.
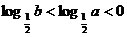
C. 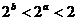 D.
D.
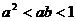
4. 已知函数 ,其导数
,其导数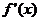 的图象如右图,
的图象如右图,
则函数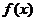 的极小值是
的极小值是
A. B.
B. C.
C. D.
D.
5. 在△ 中,若
中,若 ,则
,则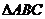 是
是
A.直角三角形 B. 等腰直角三角形
C.钝角三角形 D. 等边三角形
6. 函数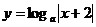 在(-2,0)上是单调递增的,则此函数在
在(-2,0)上是单调递增的,则此函数在 上是
上是
A.单调递增 B.单调递减 C.先增后减 D.先减后增
7. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文 ,
, ,
, 对应密文
对应密文 ,
, ,
, .例如,明文1,2,3对应密文7,14,6. 当接收方收到密文16,30,14时,则解密得到的明文为
.例如,明文1,2,3对应密文7,14,6. 当接收方收到密文16,30,14时,则解密得到的明文为
A.2,4,7 B.2,7,
8. 数列 中,
中,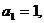
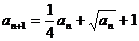 ,则
,则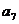 =
=
A. 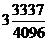 B.
B.
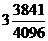 C.
C. 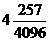 D.
D. 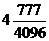
9. 已知命题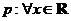 ,
, ,则
,则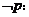 .
.
10. 已知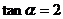 ,则
,则 .
.
11. 数列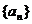 中,
中, ,且数列
,且数列 是等差数列,则
是等差数列,则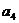 =___________.
=___________.
12. 已知函数
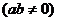 的一条对称轴方程为
的一条对称轴方程为 ,则函数
,则函数 的位于对称轴
的位于对称轴 左边的第一个对称中心为
.
左边的第一个对称中心为
.
13. 给出下列四个命题:
①函数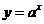 (
(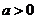 且
且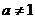 )与函数
)与函数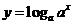 (
(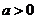 且
且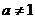 )的定义域相同;
)的定义域相同;
②函数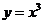 与
与 的值域相同;
的值域相同;
③函数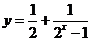 与
与 都是奇函数;
都是奇函数;
④函数 与
与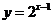 在区间
在区间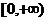 上都是增函数,
上都是增函数,
其中正确命题的序号是 .(把你认为正确的命题序号都填上)
14. 对于函数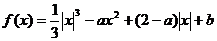 ,若
,若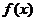 有六个不同的单调区间,则
有六个不同的单调区间,则 的取值范围为
.
的取值范围为
.
15. (本小题满分12分)
已知函数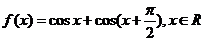
(Ⅰ)求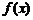 的最小正周期;
的最小正周期;
(Ⅱ)求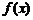 的单调增区间;
的单调增区间;
(Ⅲ)若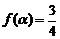 ,求
,求 的值.
的值.
16. (本小题满分12分)
已知数列 的前n项和为
的前n项和为 ,
, .
.
(Ⅰ)求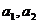 ;(Ⅱ)求数列
;(Ⅱ)求数列 的通项公式.
的通项公式.
17. (本小题满分14分)
设函数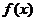 的定义域为
的定义域为 ,对任意实数
,对任意实数 、
、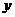 都有
都有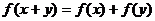 ,当
,当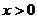 时
时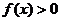 且
且 .
.
(Ⅰ) 求证:函数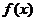 为奇函数;
为奇函数;
(Ⅱ) 证明函数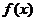 在
在 上是增函数;
上是增函数;
(Ⅲ) 在区间[-4,4]上,求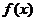 的最值.
的最值.
18. (本小题满分14分)
为庆祝东莞中学105周年,教师足球队与学生足球队进行一场足球对抗赛.
学生甲带着球,以 方向走,学生甲想离学生乙最近的时候把球传给他.问经过多少时间后,两位学生相距最近,并求出两位学生的最近距离.
方向走,学生甲想离学生乙最近的时候把球传给他.问经过多少时间后,两位学生相距最近,并求出两位学生的最近距离.
19. (本小题满分14分)
设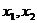 是函数
是函数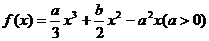 的两个极值点,且
的两个极值点,且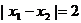 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)求 的最大值.
的最大值.
20. (本小题满分14分)
已知等差数列 满足
满足 ,等比数列
,等比数列 前
前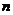 项和
项和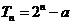 。
。
(Ⅰ) 求 的值以及数列
的值以及数列 的通项公式;
的通项公式;
(Ⅱ)试求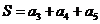 的最大值以及
的最大值以及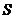 最大时数列
最大时数列 的通项公式;
的通项公式;
(Ⅲ)若 ,求数列
,求数列 的前
的前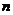 项和.
项和.

 2008届六校第二次联考
2008届六校第二次联考
理科数学答题卷
题号
一
二
三
总 分
15
16
17
18
19
20
得分
第Ⅰ卷(本卷共计40分)
题 号
1
2
3
4
5
6
7
8
选 项
第Ⅱ卷(本卷共计110分)
9. 10.
11. 12.
13. 14.
15.(本小题满分12分)
16.(本小题满分12分)
17.(本小题满分14分)
18.(本小题满分14分)
19.(本小题满分14分)
20.(本小题满分14分)
2008届六校第二次联考

