1.集合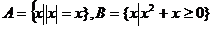 ,则
,则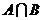 等于
等于
A.[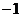 ,0] B.[0,
,0] B.[0,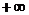
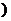 C.[1,
C.[1,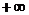
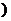 D.
D.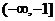
2.若函数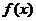 的反函数为
的反函数为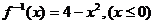 ,则
,则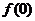 等于
等于
A.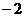 B
B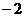 D.4
D.4
3.设映射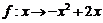 是实数集
是实数集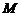 到实数集
到实数集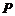 的映射,若对于实数
的映射,若对于实数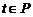 ,
,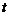 在
在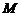 中不存在原象,则
中不存在原象,则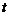 的取值范围是
的取值范围是
A.[1,+∞) B.(1,+∞) C.(-∞,1) D.(-∞,1]
4“同一首歌”心连心文艺团体下基层进行宣传演出,原准备的节目表中有6个节目,如果保持这些节目的相对顺序不变,在它们之间再插入3个舞蹈节目,如果这三个舞蹈节目在节目表中既不排头,也不排尾,则不同的插入方法有( )种
A.200 B
5.函数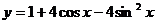
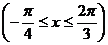 ,有
,有
A.最大值5,最小值―4 B.最大值5,最小值―3
C.最大值0,最小值―8 D.最大值2,最小值―3
6.圆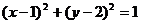 与圆
与圆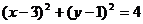 的公切线共有
的公切线共有
A.1条 B.2条 C.3条 D.4条
7.将点P(1,2)按向量a=(3,4)平移到点P′(-t2+t+6,t2+t),则实数t的值为
A.2或-1 B.-3或2
C.-1或3 D.2
8.等差数列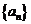 中,
中,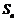 是其前
是其前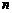 项和,
项和,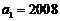 ,
,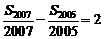 ,则
,则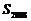 的值为
的值为
A. 2006
B
9.设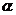 、
、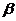 、
、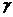 为三个不同的平面,
为三个不同的平面,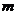 、
、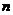 为两条不同的直线,在下列四个条件中:①
为两条不同的直线,在下列四个条件中:①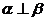 ,
,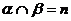 ,
,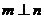 ; ②
; ②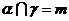 ,
,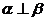 ,
,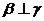 ;③
;③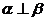 ,
,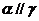 ,
,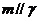 ; ④
; ④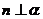 ,
,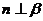 ,
,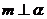 。是
。是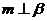 的充分条件的有:
的充分条件的有:
A.①② B.②④ C.②③ D. ③④
10.已知实数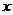 ,
,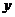 满足不等式组
满足不等式组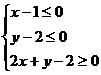 ,则
,则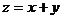 的取值范围是
的取值范围是
A.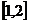 B.
B.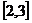 C.
C.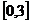 D.
D. 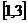
11.已知函数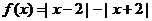 ,则使得
,则使得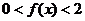 的
的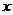 的取值范围是
的取值范围是
A.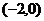 B.
B.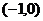 C.
C.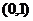 D.
D.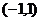
12.若F(c,0)是椭圆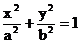 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于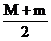 的点的坐标是
的点的坐标是
A.(c,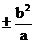 ) B.(-c,
) B.(-c,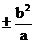 ) C.(0,±b) D.不存在
) C.(0,±b) D.不存在
第Ⅱ卷(非选择题,共90分)
13. 半径为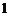 的球面上有
的球面上有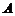 、
、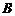 、
、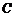 三点,其中点
三点,其中点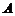 与
与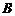 、
、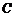 两点间的球面距离均为
两点间的球面距离均为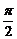 ,
,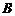 、
、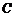 两点间的球面距离均为
两点间的球面距离均为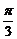 ,则球心到平面
,则球心到平面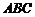 的距离为__ __ _.
的距离为__ __ _.
14. 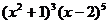 展开式中,所有项的系数之和为 .
展开式中,所有项的系数之和为 .
15.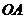 、
、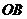 (
(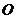 为原点)是圆
为原点)是圆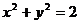 的两条互相垂直的半径,
的两条互相垂直的半径,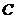 是该圆上任一点,且
是该圆上任一点,且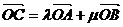 ,则
,则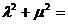 .
.
16.已知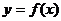 为周期函数,命题:①函数
为周期函数,命题:①函数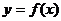 必有对称轴;②函数
必有对称轴;②函数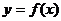 必有对称中心;③函数
必有对称中心;③函数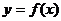 可能有对称轴又有对称中心;④
可能有对称轴又有对称中心;④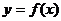 可能既无对称轴又无对称中心。其中不正确的是命题的序号为_ __.
可能既无对称轴又无对称中心。其中不正确的是命题的序号为_ __.
17.(本小题满分10分)
已知点A(2,0),B(0,2),C(cos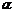 ,sin
,sin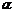 ),且0<
),且0<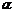 <
<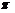 。
。
(1)若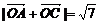 ,求
,求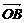 与
与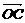 的夹角;
的夹角;
(2)若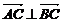 ,求tan
,求tan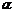 的值。
的值。
18.(本小题满分10分)
食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测.如果四项指标中的第四项不合格或其它三项指标中有两项不合格,则这种品牌的食品不能上市.已知每项检测是相互独立的,第四项指标抽检出现不合格的概率是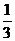 ,且其它三项指标抽检出现不合格的概率均是
,且其它三项指标抽检出现不合格的概率均是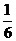 ・
・
(1)若食品监管部门要对其四项质量指标依次进行严格的检测,求恰好在第三项指标检测结束时,能确定该食品不能上市的概率;
 (2)求该品牌的食品能上市的概率.
(2)求该品牌的食品能上市的概率.
19. (本小题满分12分)
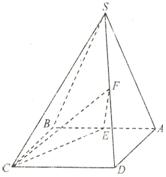
如图,四棱锥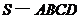 的底面
的底面
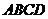 是正方形,侧面
是正方形,侧面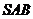 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,
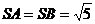 ,
,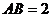 ,
,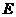 、
、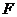 分别是
分别是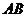 、
、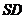 的中点。
的中点。
(1)求证: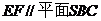 ;
;
(2)求二面角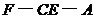 的大小。
的大小。
20.(本小题满分12分)
设数列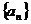 的前n项和为
的前n项和为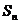 ,且
,且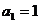 ,
,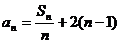 (
(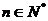 )
)
(1)求证:数列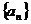 为等差数列,并求出
为等差数列,并求出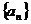 的通项公式;
的通项公式;
(2)设数列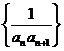 的前n项和
的前n项和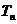 ,证明:
,证明: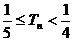 ;
;
21. (本小题满分12分)
在平面直角坐标系xOy中,经过点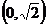 且斜率为
且斜率为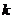 的直线
的直线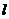 与椭圆
与椭圆
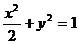 有两个不同的交点P和Q。
有两个不同的交点P和Q。
(1)求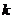 的取值范围;
的取值范围;
(2)设椭圆与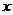 轴正半轴、
轴正半轴、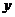 轴正半轴的交点分别为A、B,是否存在常数
轴正半轴的交点分别为A、B,是否存在常数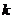 ,使得向量
,使得向量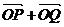 与
与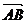 共线?如果存在,求
共线?如果存在,求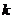 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
22、(本小题满分12分)
已知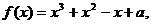 (其中
(其中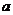 为常数,
为常数,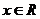 )
)
(1)求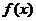 的极值;
的极值;
(2)若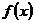 的图象与
的图象与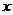 轴只有一个交点,求
轴只有一个交点,求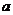 的取值范围.
的取值范围.
2009届高考调研试题数学 (文史类)

