11.已知三角形的三边长为3,5,x 则第三边x的取值范围是 .
.
 12.图5的围棋盘放置在某个平面直角坐标系内,白棋②的坐标为 (-7,-4),
12.图5的围棋盘放置在某个平面直角坐标系内,白棋②的坐标为 (-7,-4),
白棋④的坐标为(-6,-8),那么黑棋①的坐标应该是  .
.
 13.如图6,现有一圆心角为90°,半径为
13.如图6,现有一圆心角为90°,半径为
用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底
面圆的半径为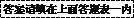 .
.
14.瑞士中学教师巴尔末成功地从光谱数据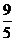 ,
,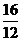 ,
,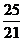 ,
,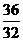 ,……中得到巴尔末公式,从而打开了光谱奥妙的大门,请按这种规律写出第七个数据是
,……中得到巴尔末公式,从而打开了光谱奥妙的大门,请按这种规律写出第七个数据是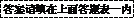 .
.
 15.如图7,将半径为
15.如图7,将半径为
和
的路线长度是 cm. (精确到
cm. (精确到
|

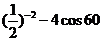 °
°
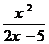 +
+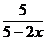 =1
=1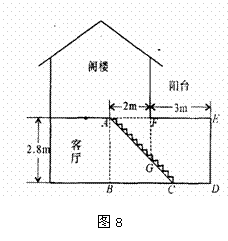 (2)(3分)在(1)的条件下,为保证上楼时的舒适感,楼梯的每个台阶高小于
(2)(3分)在(1)的条件下,为保证上楼时的舒适感,楼梯的每个台阶高小于 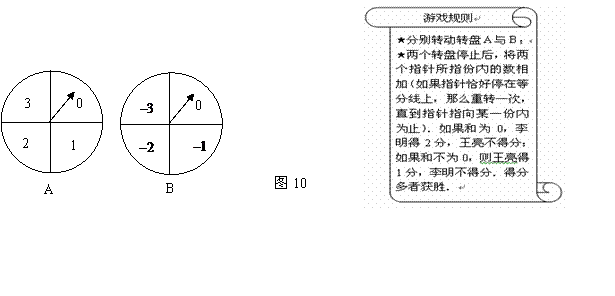 (1)(4分)用树状图或列表法,求两数相加和为零的概率;
(1)(4分)用树状图或列表法,求两数相加和为零的概率;
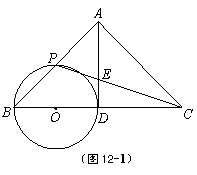
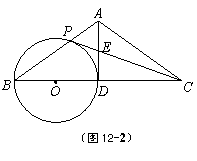
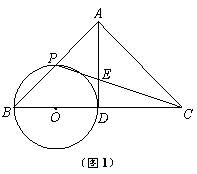 21.(10分) 已知:如图12-1,在△ABC中,AB = AC,点D是边BC的中点.以BD为直径作圆O,交边AB于点P,联结PC,交AD于点E.
21.(10分) 已知:如图12-1,在△ABC中,AB = AC,点D是边BC的中点.以BD为直径作圆O,交边AB于点P,联结PC,交AD于点E.