1.设集合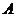 、
、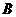 是全集
是全集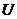 的两个子集,则“
的两个子集,则“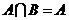 ”是“
”是“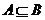 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.若复数z满足z(1+i)=2i,则复数z的实部与虚部之和为
A.2
B.
3.已知数列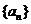 的通项
的通项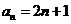 ,前
,前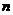 项和为
项和为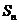 ,若数列
,若数列 的前
的前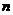 项和
项和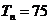 ,则
,则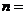
A.8
B.
A.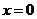 B.
B.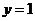 C.
C.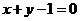 D.
D.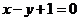
5.已知定义在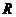 上的函数
上的函数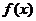 为奇函数,且当
为奇函数,且当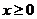 时
时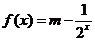 ,则
,则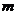 的值为
的值为
A.0
B.
6.在5张卡片上分别写着1、2、3、4、5,混合后再任意排成一行,则得到的五位数能被2或5整除的概率为
A.0.2
B.
7.若定义在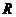 上的偶函数
上的偶函数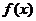 的最小正周期是
的最小正周期是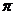 ,且当
,且当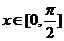 时,
时,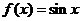 ,则
,则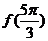 的值为
的值为
A.1
B.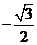 C.
C.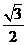 D.
D.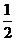
8.下列结论中正确的是
A.当x > 0且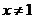 时,
时,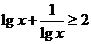 B.当x > 0时,
B.当x > 0时,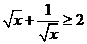
C.当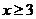 时,
时, 的最小值是2
D.当
的最小值是2
D.当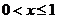 时,
时,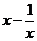 无最大值
无最大值
9.已知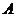 、
、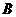 两点的坐标分别为
两点的坐标分别为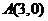 、
、 ,
,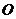 是原点,点
是原点,点 在线段
在线段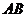 上,若
上,若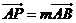
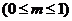 ,则
,则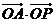 的取值范围是
的取值范围是
A.(1,9) B.(0,9) C.[0,9] D.[1,9]
10.已知双曲线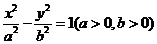 的右焦点为
的右焦点为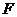 ,若过点
,若过点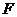 且倾斜角为60°的直线与双曲线渐近线平行,则此双曲线离心率的值为
且倾斜角为60°的直线与双曲线渐近线平行,则此双曲线离心率的值为
A.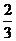 B.
B. D.3
D.3
11.在实数集上定义运算: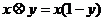 ,
,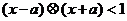 若不等式对任意实数x都成立,则实数a的取值范围是
若不等式对任意实数x都成立,则实数a的取值范围是
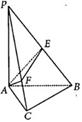 A.
A.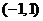 B.
B. C.
C.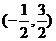 D.
D.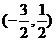
12.如图,在三棱锥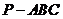 中,
中,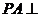 底面
底面 ,
,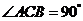 ,
,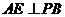
于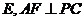 于
于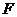 ,若
,若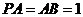 ,则当
,则当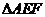 的面积最大时,
的面积最大时,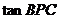
等于
A.2
B.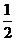 C.
C.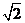 D.
D.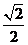
第Ⅱ卷
(本卷共10小题,共90分)
注意事项:
1.考生不能将答案直接答在试卷上,必须答在答题卡上。
13.设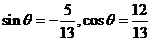 ,则
,则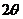 的终边所在象限是第______________象限。
的终边所在象限是第______________象限。
14.在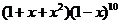 的展开式中,含
的展开式中,含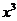 项的系数是_____________。
项的系数是_____________。
15.若实数 满足
满足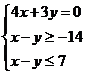 ,则
,则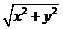 的取值范围是_____________。
的取值范围是_____________。
16.若等比数列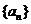 中,
中,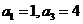 ,则
,则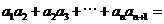 ___________。
___________。
17.(本小题满分10分)
已知向量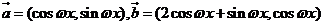 ,其中
,其中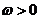 ,
,
记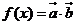 ,若函数
,若函数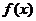 的最小正周期是
的最小正周期是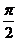 。
。
(I)求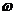 的值;
的值;
(Ⅱ)求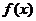 的最小值和使
的最小值和使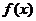 取得最小值的
取得最小值的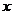 的集合。
的集合。
18.(本小题满分12分)
汉方集团用三辆客车送职工去黄果树旅游,从贵阳到黄果树有清黄高速公路和贵黄高等
级公路两条公路,已知客车走贵黄公路堵车的概率为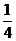 ;若1号、2号两辆客车走贵黄公路。
;若1号、2号两辆客车走贵黄公路。
3号客车走清黄公路,且三辆客车是否堵车相互之间没有影响,若三辆客车中恰有一辆被堵
车的概率为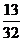
(I)求客车走清黄公路堵车的概率;
(Ⅱ)求三辆客车中被堵车辆的辆数的数学期望和方差。
19.(本小题满分12分)
如图,在三棱柱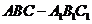 中,所有的棱长都为2,
中,所有的棱长都为2,
侧面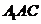 与底面
与底面 垂直,
垂直,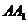 与底面
与底面 所成角为
所成角为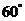 。
。
(I)求证: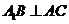 ;
;
(Ⅱ)求平面 与平面
与平面 所成的二面角(锐角)的大
所成的二面角(锐角)的大
小
20.(本小题满分12分)
已知等差数列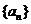 中
中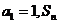 为前
为前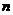 项和,且
项和,且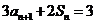 。
。
(I)求数列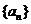 的通项公式;
的通项公式;
(Ⅱ)记 若对任意的正整数
若对任意的正整数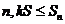 恒成立,求实数
恒成立,求实数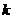 的最大值。
的最大值。
21.(本小题满分12分)
设函数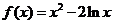 。
。
(I)求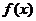 的最小值;
的最小值;
(Ⅱ)当 时,若
时,若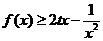 在
在 内恒成立,求
内恒成立,求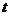 的取值范围。
的取值范围。
 22.本小题满分12分
22.本小题满分12分
已知圆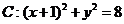 ,定点
,定点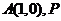 为圆上一
为圆上一
动点,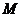 是
是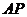 的中点,点
的中点,点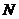 在
在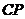 上,若
上,若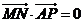 ,
,
(I)求点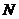 的轨迹
的轨迹 的方程;
的方程;
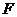 、
、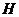 ,
,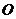 是坐标原点,
是坐标原点,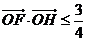 ,求
,求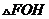 的面积的最小值。
的面积的最小值。

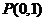 与圆
与圆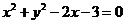 相交的所有
相交的所有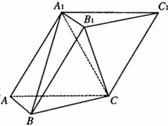
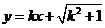 与曲线
与曲线




