1.若将复数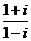 表示为
表示为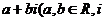 是虚数单位)的形式,则
是虚数单位)的形式,则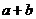 等于
等于
A.0
B.
 2.已知集合
2.已知集合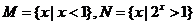 ,则
,则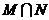 等于
等于
A.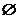 B.
B.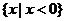
C.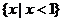 D.
D.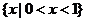
3.设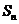 是等差数列
是等差数列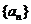 的前
的前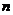 项和,若
项和,若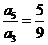 ,则
,则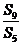 =
=
A.1
B.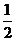
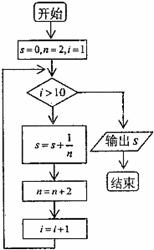
4.如图,程序框图所进行的求和运算是
A.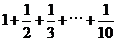
B.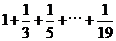
C.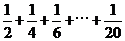
 D.
D.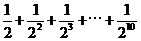
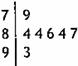
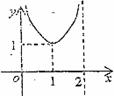
5.右图是某学校举行的运动会上,七位评委为某体操项目打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数的方差分别为
A.84,4.84 B.84,1.6
 C.85,1.6
D.85,4
C.85,1.6
D.85,4
6.函数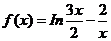 的零点一定位于区间
的零点一定位于区间
A.(1,2) B.(2,3) C.(3,4) D.(4,5)
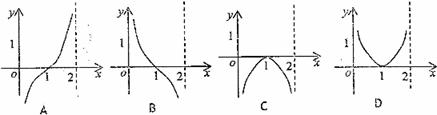
7.函数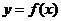 的图象如右图所示,
的图象如右图所示,
则函数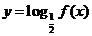 的图象大致是
的图象大致是
8.已知函数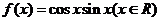 ,给出下列四个命题:
,给出下列四个命题:
①若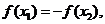 则
则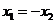 ; ②
; ②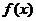 的最小正周期是2
的最小正周期是2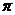 ;
;
③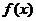 在区间
在区间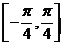 上是增函数; ④
上是增函数; ④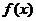 的图象关于直线
的图象关于直线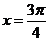 对称
对称
A.①②④ B.①③ C.②③ D.③④
9.若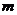 、
、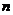 是两条不同的直线,
是两条不同的直线,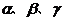 是三个不同的平面,则下列命题中为真命题的是
是三个不同的平面,则下列命题中为真命题的是
A.若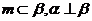 ,则
,则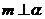 B.若
B.若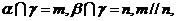 则
则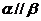
C.若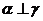 ,
,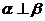 ,则
,则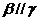 D.若
D.若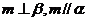 ,则
,则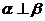
10.已知向量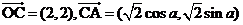 ,则向量
,则向量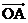 的模的最大值是
的模的最大值是
A.3
B.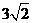 C.
C.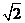 D.18
D.18
11.已知圆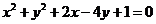 关于直线
关于直线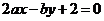
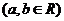 对称,则
对称,则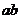 的取值范围是
的取值范围是
A.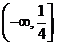 B.
B.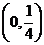 C.
C.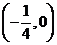 D.
D.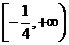
12.若函数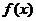 为奇函数,且在
为奇函数,且在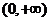 内是增函数,又
内是增函数,又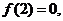 则
则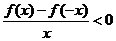 的解集为
的解集为
A.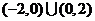 B.
B.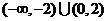
C.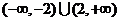 D.
D.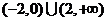
第Ⅱ卷(共90分)
注意事项:
第Ⅱ卷共2页。考生必须使用0.5毫米黑色签字笔在答题卡上题目的指定答题区域内作
答,填空题请直接写答案,解答题应写出文字、证明过程或演算步骤。在试卷上作答无效。
13.抛物线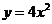 的焦点坐标是__________。
的焦点坐标是__________。
14.已知正方体外接球的体积是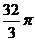 ,则正方体的棱长等于__________。
,则正方体的棱长等于__________。
15.若函数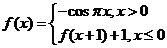 则
则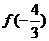 的值为___________。
的值为___________。
16.给出下列四个命题:
①若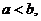 则
则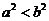 ;
;
②若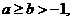 则
则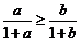 ;
;
③若正整数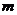 和
和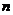 满足;
满足;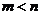 ,则
,则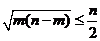 ;
;
④若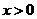 ,且
,且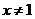 ,则
,则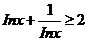 ;
;
其中真命题的序号是_______________________(请把真命题的序号都填上)。
17.(本小题满分12分)
已知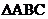 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为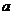 、
、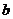 、
、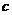 ,且满足
,且满足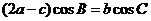 。
。
(1)求角B大小;
(2)设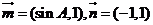 ,求
,求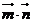 的最小值。
的最小值。
18.(本小题满分12分)
已知数列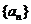 的各项均为正数,
的各项均为正数,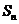 为其前
为其前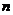 项和,对于任意的
项和,对于任意的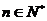 满足关系式
满足关系式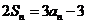 。
。
(1)求数列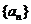 的通项公式;
的通项公式;
(2)设数列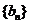 的通项公式是
的通项公式是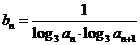 ,前
,前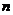 项和为
项和为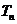 ,
,
求证:对于任意的正整数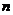 ,总有
,总有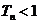 。
。
19.(本小题满分12分)
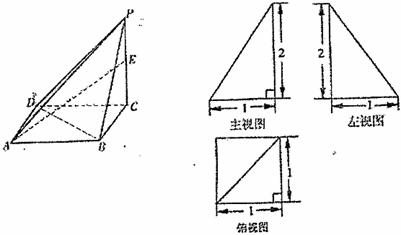
已知四棱锥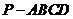 的三视图如下。
的三视图如下。
(I)求四棱锥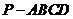 的体积;
的体积;
(Ⅱ)若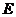 是侧棱
是侧棱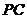 的中点,求证:
的中点,求证: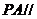 平面
平面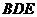 ;
;
(Ⅲ)若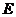 是侧棱
是侧棱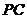 上的动点,不论点
上的动点,不论点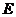 在何位置,是否都有
在何位置,是否都有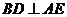 ?证明你的
?证明你的
结论。
20.(本小题满分12分)
班级联欢时,主持人拟出了如下一些节目:跳双人舞、独唱、朗诵等,指定3个男生和2个女生来参与,把5个人分别编号为1,2,3,4,5,其中1,2,3号是男生,4,5号是女生,将每个人的号分别写在5张相同的卡片上,并放入一个箱子中充分混合,每次从中随即地取出一张卡片,取出谁的编号谁就参与表演节目。
(I)为了选出2人来表演双人舞,连续抽取2张卡片,求取出的2人不全是男生的概率;
(Ⅱ)为了选出2人分别表演独唱和朗诵,抽取并观察第一张卡片后,又放回箱子中,充分混合后再从中抽取第二张卡片,求:独唱和朗诵由同一个人表演的概率。
21.(本小题满分12分)
已知函数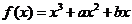 。
。
(I)若函数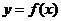 在
在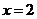 处有极值-6,求
处有极值-6,求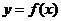 的单调递减区间;
的单调递减区间;
(Ⅱ)若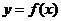 的导数
的导数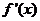 对
对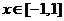 都有
都有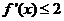 ,求
,求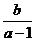 的范围。
的范围。
22.(本小题满分14分)
已知离心率为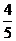 的椭圆的中心在原点,焦点在
的椭圆的中心在原点,焦点在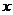 轴上,双曲线
轴上,双曲线
以椭圆的长轴为实轴,短轴为虚轴,且焦距为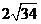 。
。
(I)求椭圆及双曲线的方程;
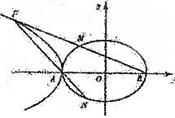
(Ⅱ)设椭圆的左、右顶点分别为A、B,在第二象限内取双曲线
上一点P,连结BP交椭圆于点M,连结PA并延长交椭圆于点N,若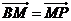 。求
。求
四边形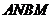 的面积。
的面积。